La funzione 
è definita da ![f(x)=\int_0^x [ cos(\frac t2 + \frac 12) ] dt](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-914f5508d9020a16c78ee47f087d7892_l3.png "Rendered by QuickLaTeX.com")
per tutti i numeri reali 
appartenenti
all’intervallo chiuso [0, 9].
- Sia R la regione del piano delimitata da Σ e dall’asse per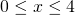
; 
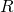è la base di un solido 
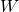le cui sezioni con piani ortogonali all’asse hanno, per ciascun , area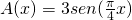 
. Si calcoli il volume di W.
Il volume di è dato dal risultato dell’integrale:
![\[V(W)=\int_0^4 A(x)dx=\int_0^4 3 sen(\frac {\pi}{4}x)dx=3 \big[-\frac {4}{\pi}cos(\frac {\pi}{4}x)\big]_0^4=\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-d6c4973750ae73521ab66199a7c78608_l3.png "Rendered by QuickLaTeX.com")
![\[=3[-\frac {4}{\pi}cos(\frac {\pi}{4}\cdot 4)+\frac {4}{\pi} cos(0)]=3 \cdot \frac {8}{\pi}=\frac {24}{\pi}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-33aaa1fd3cc825b36fa42fef02e6ffaa_l3.png "Rendered by QuickLaTeX.com")
.
Altri esercizi simili
- Problema 1.1 Scientifico 2013
- Problema 1.2 Scientifico 2013
- Problema 1.3 Scientifico 2013
- Problema 1.4 Scientifico 2013
(Questa pagina è stata visualizzata da 21 persone)