Una funzione ![]() è definita e derivabile, insieme alle sue derivate prima e seconda, in
è definita e derivabile, insieme alle sue derivate prima e seconda, in ![]() e nella figura sono disegnati i grafici
e nella figura sono disegnati i grafici ![]() e
e ![]() di
di ![]() e della sua derivata seconda
e della sua derivata seconda ![]() . La tangente a
. La tangente a ![]() nel suo punto di flesso, di coordinate (2; 4) , passa per (0; 0), mentre le rette
nel suo punto di flesso, di coordinate (2; 4) , passa per (0; 0), mentre le rette ![]() e
e ![]() sono asintoti orizzontali per
sono asintoti orizzontali per ![]() e
e ![]() , rispettivamente.
, rispettivamente.
Si dimostri che la funzione ![]() , ovvero la derivata prima di f (x) , ha un massimo e se ne determinino le coordinate. Sapendo che per ogni
, ovvero la derivata prima di f (x) , ha un massimo e se ne determinino le coordinate. Sapendo che per ogni ![]() del dominio è:
del dominio è: ![]() , qual è un possibile andamento di
, qual è un possibile andamento di ![]() ?
?
Analizziamo per prima cosa come si comportano le funzioni nel punto F di coordinate ![]() .
.
Visto che F è un punto di flesso, ovvero ![]() , e che
, e che ![]() è la derivata di
è la derivata di ![]() , possiamo affermare che in
, possiamo affermare che in ![]() c’è un punto stazionario di
c’è un punto stazionario di ![]() .
.
Osservando il grafico, notiamo che ![]() ha segno positivo per
ha segno positivo per ![]() , mentre per
, mentre per ![]() ha segno negativo: perciò, ricordando che
ha segno negativo: perciò, ricordando che ![]() è la derivata di
è la derivata di ![]() , possiamo concludere che
, possiamo concludere che ![]() ha un andamento crescente per
ha un andamento crescente per ![]() e un andamento decrescente per
e un andamento decrescente per ![]() . Quindi, in
. Quindi, in ![]() abbiamo un punto di massimo.
abbiamo un punto di massimo.
Ora, dobbiamo trovare il valore della coordinata ![]() del punto di massimo.
del punto di massimo.
Prima di calcolarlo dobbiamo ricordarci del significato geometrico della derivata, ovvero ![]() è la funzione che esprime i valori dei coefficienti angolari delle rette tangenti a
è la funzione che esprime i valori dei coefficienti angolari delle rette tangenti a ![]() nei punti di ascissa
nei punti di ascissa ![]() . Quindi
. Quindi ![]() è il valore del coefficiente angolare della retta tangente a
è il valore del coefficiente angolare della retta tangente a ![]() nel punto di ascissa
nel punto di ascissa ![]() .
.
Non conoscendo l’equazione della retta tangente, ma sapendo che passa per i punti F e O, quindi possiamo calcolare il valore di m attraverso la formula
![]()
Quindi possiamo concludere che ![]() e che quindi il punto di massimo di
e che quindi il punto di massimo di ![]() è
è ![]() .
.
Quindi, dopo aver capito che:
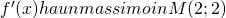 ;
;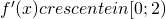
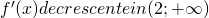 ,
,
studiamo cosa succede a ![]() agli estremi del dominio.
agli estremi del dominio.
Poichè per ipotesi vale la relazione ![]() , per
, per ![]() ,
, ![]() è decrescente e
è decrescente e ![]() , possiamo affermare che:
, possiamo affermare che:
![]()
Inoltre, sempre osservando il grafico di ![]() , notiamo che la curva ha un punto di minimo P, quindi la sua derivata prima
, notiamo che la curva ha un punto di minimo P, quindi la sua derivata prima ![]() . Visto che
. Visto che ![]() equivale alla funzione derivata seconda di
equivale alla funzione derivata seconda di ![]() , nel punto P,
, nel punto P, ![]() avrà flesso e quindi cambio di concavità. E dato che nell’intervallo
avrà flesso e quindi cambio di concavità. E dato che nell’intervallo ![]() la funzione
la funzione ![]() è decrescente, allora
è decrescente, allora ![]() è negativa e quindi la
è negativa e quindi la ![]() avrà una concavità diretta verso il basso, mentre nell’intervallo
avrà una concavità diretta verso il basso, mentre nell’intervallo ![]() sarà esattamente il contrario e avrà la concavità diretta verso l’alto.
sarà esattamente il contrario e avrà la concavità diretta verso l’alto.
Per stabilire il valore di partenza, ovvero ![]() non abbiamo le informazioni necesarie, ma sappiamo per certo che
non abbiamo le informazioni necesarie, ma sappiamo per certo che ![]() . Quindi il grafico sarà:
. Quindi il grafico sarà:
Altri esercizi simili
(Questa pagina è stata visualizzata da 4 persone)
