Problema 1 P.N.I. 2012

0

Della funzione f, definita per 0 \leq x \leq 6 , si sa che è dotata di derivata prima e seconda e che il grafico della sua  derivata f '(x), disegnato a lato, presenta due tangenti orizzontali per x = 2 e x = 4. Si sa anche che f (0) = 9, f (3) = 6 e f (5) = 3.

 

  1. Si trovino le ascisse dei punti di flesso di 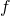f motivando le risposte in modo esauriente.
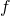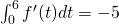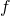  2. Per quale valore di x la funzione f presenta il suo minimo assoluto? Sapendo che \int_0^6f'(t)dt=-5 per quale valore di x la funzione f presenta il suo massimo assoluto?
  3. Sulla base delle informazioni note, quale andamento potrebbe avere il grafico di f ?
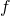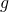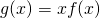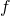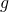  4. Sia g la funzione definita da g(x) = x f (x). Si trovino le equazioni delle rette tangenti ai grafici di f e di g nei rispettivi punti di ascissa 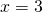x = 3 e si determini la misura, in gradi e primi sessagesimali, dell’angolo acuto che esse formano.

 

 

 

Altri esercizi simili

(Questa pagina è stata visualizzata da 21 persone)

Lascia un commento