Siano ![]() e
e ![]() le funzioni definite, per tutti gli x reali, da
le funzioni definite, per tutti gli x reali, da
![]()
- Si scrivano le equazioni delle rette
 e
e  tangenti, rispettivamente, a
tangenti, rispettivamente, a 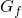 e a
e a 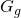 nel punto di ascissa
nel punto di ascissa 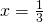 . Qual è l’ampiezza, in gradi e primi sessagesimali, dell’angolo acuto formato da
. Qual è l’ampiezza, in gradi e primi sessagesimali, dell’angolo acuto formato da  e da
e da  ?
?
Notiamo che ![]() e
e ![]() si intersecano per
si intersecano per ![]() nel punto di ordinata 1.
nel punto di ordinata 1.
Possiamo calcolare i coefficienti angolari delle rette tangenti ad ![]() e
e ![]() in
in ![]() grazie alle derivate
grazie alle derivate ![]() e
e ![]() .:
.:
![]()
![]()
Pertanto la retta ![]() ha equazione:
ha equazione:
![]()
la retta ![]() ha equazione:
ha equazione:
![]()
Osserivamo che la retta ![]() è parallela all’asse
è parallela all’asse ![]() , pertanto l’angolo richiesto è uguale all’angolo
, pertanto l’angolo richiesto è uguale all’angolo ![]() che la retta
che la retta ![]() forma con l’asse delle
forma con l’asse delle ![]() . Sappiamo che la tangente di tale angolo è uguale al coefficiente angolare della retta
. Sappiamo che la tangente di tale angolo è uguale al coefficiente angolare della retta ![]() , dunque:
, dunque:
![]()
Altri esercizi simili
- Problema 1.1 Scientifico 2012
- Problema 1.2 Scientifico 2012
- Problema 1.3 Scientifico 2012
- Problema 1.4 Scientifico 2012
(Questa pagina è stata visualizzata da 14 persone)