Siano 
e 
le funzioni definite, per tutti gli x reali, da
![\[f(x)=|27x^3| \quad \quad \mbox { e } \quad \quad g(x)= sen \left( \frac 32 \pi x\right).\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-3286eab79fae1f7bcc41c6ff142e3bef_l3.png "Rendered by QuickLaTeX.com")
- Sia R la regione delimitata 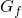da
e da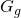 
. Si calcoli l’area di R.
L’area della regione R è data dalla differenza tra l’area sottesa da e l’area sottesa da nell’intervallo ![\left[0; \frac 13 \right]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-d222a662d2e9f86aa0dc6ab202dbf88c_l3.png "Rendered by QuickLaTeX.com")
:
![\[\int_0^\frac 13 sen\left (\frac 32 \pi x \right) dx - \int_0^\frac 13 27x^3 dx= \left[ -\frac {2}{3\pi} cos \left (\frac 32 \pi x \right)\right] - \left[ \frac {27}{4}x^4\right]_0^\frac 13=\frac {2}{3\pi} - \frac {1}{12}=\frac {8-\pi}{12\pi}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-c96522608cab3d187ad2a6791ae56c1a_l3.png "Rendered by QuickLaTeX.com")
.
Altri esercizi simili
- Problema 1.1 Scientifico 2012
- Problema 1.2 Scientifico 2012
- Problema 1.3 Scientifico 2012
- Problema 1.4 Scientifico 2012
(Questa pagina è stata visualizzata da 9 persone)