Problema 1.2 P.N.I. 2012

Della funzione $f$ , definita per $0 \leq x \leq 6$ , si sa che è dotata di derivata prima e seconda e che il grafico della sua derivata $f '(x)$ , disegnato a lato, presenta due tangenti orizzontali per $x = 2$ e $x = 4$ . Si sa anche che $f (0) = 9$ , $f (3) = 6$ e $f (5) = 3$ .

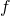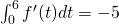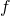Per quale valore di $x$ la funzione $f$ presenta il suo minimo assoluto? Sapendo che $\int_0^6f'(t)dt=-5$ per quale valore di $x$ la funzione $f$ presenta il suo massimo assoluto?

Dal grafico della derivata osserviamo che:

$f'(x) \leq 0 \mbox { se } x \in [0;5] \quad \mbox { e } \quad f'(x) \geq 0 \mbox { se } x \in [5;6].$

Da questo deduciamo che f è decrescente nell’intervallo [0;5] e crescente in [5;6]. Quindi la funzione $f$ ammetterà punto di minimo in corrispondenza di $x=5$ .

Quindi, si nota anche che il punto di massimo assoluto la funzione lo può avere solo agli estremi del dominio, e quindi dovremo confrontare i valori assunti dalla funzione nei punti di ascissa 0 e 6.

Poichè $f'$ è derivata di $f$ , abbiamo che $f$ è per definizione una primitiva di $f'$ . Sfruttando il teorema fondamentale del calcolo integrale, otteniamo che: