Problema 1.1 Scientifico 2011

Si considerino le funzioni $f$ e $g$ definite, per tutti gli $x$ reali, da:

$f (x) = x^3 - 4x \quad \quad \mbox { e } \quad \quad g (x) = sen (\pi x).$

Fissato un conveniente sistema di riferimento cartesiano $Oxy$ , si studino $f$ e $g$ e se ne disegnino i rispettivi grafici $G_f$ e $G_g$ .

Studiamo le due funzioni separatamente:
$f(x) = x^3 - 4x$

Essendo una funzione razionale intera, sappiamo per certo che sarà definita per ogni $x$ reale, quindi:

$D= R$

Analizziamo le possibili simmetrie:

$f(−x) = − x^3 + 4x = − f(x)$ ,

quindi la funzione è dispari, ma questo lo si poteva capire da subito essendo una funzione polinomiale dove le incognite assumono solo esponenti dispari.

Le intersezioni con gli assi sono:

Asse y: 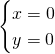$\begin {cases} x=0 \\ y=0 \end { cases}$

Asse x : $\begin {cases} y=0 \\ x(x^2-4)=0 \end { cases} \iff \begin {cases} y=0 \\ x=0 , x=\pm2 \end { cases}$ .

Quindi intersecherà gli assi coordinati in 3 punti:

o(0;0) , A(2;0) , B(-2;0).

Vediamo dove la funzione risulta essere positiva:

$f(x) >0 \iff x(x^2-4) >0 \iff x(x+2)(x-2) >0 \iff -2<x<0 \quad \lor \quad x>2$ .

Studiamo i limiti agli estremi del dominio:

$\lim_{x \to \pm \infty} f(x)= \pm \infty$ .

Essendo una funzione polinomiale, questa non presenterà asintoti.

Analizziamo ora le derivate:

$f'(x)=3x^2-4$ ;

$f'$ risulta essere positiva (e quindi $f$ crescente) per $x< -\frac {2}{\sqrt 3}$ e per $x>\frac {2}{\sqrt 3}$ ; risulta esser negativa (quindi $f$ decrescente) per $-\frac {2}{\sqrt 3}<x<\frac {2}{\sqrt 3}$ .

Avrà massimo in $M\left ( -\frac {2}{\sqrt 3}; \frac {16}{3\sqrt 3}\right)$ , e minimo in $m\left (\frac {2}{\sqrt 3}; -\frac {16}{3\sqrt 3}\right)$ .