Un serbatoio ha la stessa capacità del cilindro di massimo volume inscritto in una sfera di raggio 60 cm. Quale è la capacità in litri del serbatoio?
Dai dati avremo che:
- Raggio della sfera
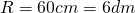 ;
; 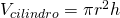 ;
;
Sia ![]() , con
, con ![]() .
.
Per il Teorema di Pitagora applicato al triangolo rettangolo AOH, avremo:
![]()
da cui ricaviamo:
![]() .
.
Calcoliamo la derivata prima così da trovare il volume massimo:
![]() .
.
![]() .
.
Dato che ![]() deve essere compreso tra 0 e 12, allora
deve essere compreso tra 0 e 12, allora ![]() è accettabile.
è accettabile.
Quindi, il volume sarà:
![]()
Altri esercizi simili
- Quesito 1 Scientifico 2011
- Quesito 2 Scientifico 2011
- Quesito 3 Scientifico 2011
- Quesito 4 Scientifico 2011
- Quesito 5 Scientifico 2011
- Quesito 6 Scientifico 2011
- Quesito 7 Scientifico 2011
- Quesito 8 Scientifico 2011
- Quesito 9 Scientifico 2011
- Quesito 10 Scientifico 2011
(Questa pagina è stata visualizzata da 2 persone)