PROBLEMA 2
Nel piano, riferito a coordinate cartesiane Oxy, si consideri la funzione f definita da ![]()
![]() .
.
Sia r la retta passante per O tangente a ![]() (e = numero di Nepero). Quale è la misura in radianti dell’angolo che la retta r forma con il semiasse positivo delle ascisse?
(e = numero di Nepero). Quale è la misura in radianti dell’angolo che la retta r forma con il semiasse positivo delle ascisse?
Chiamando Q il punto di tangenza, notiamo subito che avrà coordinate ![]() e sia r la retta passante per l’origine di equazione generica
e sia r la retta passante per l’origine di equazione generica ![]() .
.
La condizione di tangenza implica che il coefficiente angolare della retta, ovvero a, deve essere uguale alla derivata calcolata nel punto Q, ed, inoltre, ![]() .
.
Avremo:
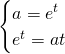
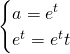
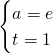
Quindi la retta ![]() risulta essere tangente alla funzione
risulta essere tangente alla funzione ![]() nel punto
nel punto ![]() .
.
Avremo dunque:
![]() .
.
Altri esercizi simili
- Problema 2.1 Scientifico 2010
- Problema 2.2 Scientifico 2010
- Problema 2.3 Scientifico 2010
- Problema 2.4 Scientifico 2010
(Questa pagina è stata visualizzata da 1 persone)