Oggetto: Equazioni con valore assoluto
Corpo del messaggio:
1)![]()
Risposta dello staff
Imponendo che ![]() , otteniamo:
, otteniamo:
![]()
Quindi avremo da risolvere due sistemi:


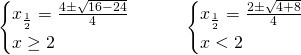
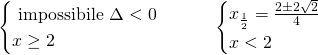
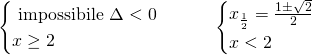
Il secondo sistema ammetterà ambedue le soluzioni, poichè ![]() .
.
Quindi l’equazione avrà come soluzioni:
![]()
(Questa pagina è stata visualizzata da 155 persone)