Oggetto:
Corpo del messaggio:
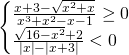
Risposta dello staff
Analizziamo pezzo per pezzo:
![]()
![]()
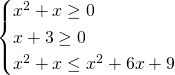
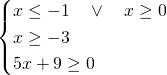
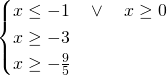
Quindi, il numeratore della prima disequazione è positivo per
![]()
e negativo per
![]() .
.
Prendiamo il primo denominatore:
![]()
![]()
![]()
![]()
Quindi sarà positivo per:
![]()
negativo per
![]()
andando a fare il grafico otteniamo che la prima disequazione è verificata per:
![]() .
.
Nel secondo sistema ci si accorge subito che il numeratore, ove verificata l’esistenza del radicando è sempre positivo, mentre il denominatore:
![]()
dobbiamo dividerlo in 3 sistemi:
![Rendered by QuickLaTeX.com \[\begin{cases} x< -3 \\ -x +x+3>0\end{cases} \quad \begin{cases} -3 \leq x< 0 \\ -x -x-3>0\end{cases} \quad \begin{cases} x>0 \\ x-x-3>0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-337eca23828d073fe6ea2fb0a8fdd892_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x< -3 \\ 3>0\end{cases} \quad \begin{cases} -3 \leq x< 0 \\ x < -\frac 32 \end{cases} \quad \begin{cases} x>0 \\ -3>0\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-6d9e109132a00124926986e9397ec836_l3.png)
che darà come risultati:
![]()
Questa, intersecata alla soluzione del numeratore ![]() , fa si che la seconda disequazione sia verificata per:
, fa si che la seconda disequazione sia verificata per:
![]()
Quindi, il sistema iniziale diventerà:
![Rendered by QuickLaTeX.com \[\begin{cases} x \leq -\frac 95 \quad \lor \quad x>1 \\ -\frac 32 <x\leq 4\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-8794187d3749f827b83f27455c2b19dc_l3.png)
che ammetterà come soluzione
![]()
(Questa pagina è stata visualizzata da 101 persone)