Oggetto:
Corpo del messaggio:
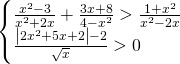
Risposta dello staff
Notiamo subito che nella seconda disequazione, il denominatore sarà sempre positivo, se la x risulta essere strettamente positiva, quindi possiamo tranquillamente inserirlo come condizione base del sistema, così da avere:
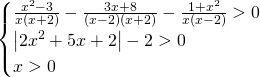
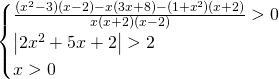
Studiamo separatamente i casi:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| -2 | 0 | 2 | ||||||
| +++ | —- | —- | —- | —- | —- | +++ | +++ | +++ |
| —- | —- | —- | —- | +++ | +++ | +++ | +++ | +++ |
| —- | —- | +++ | +++ | +++ | +++ | +++ | +++ | +++ |
| —- | —- | —- | —- | —- | —- | —- | —- | +++ |
| —- | +++ | —- | —- | +++ | +++ | —- | —- | ++++ |
Quindi la frazione sarà verificata per
![]()
![]()
![]()
![]()
Quindi il primo è verificato per ![]()
La seconda sarà impossibile.
Mettendo tutto a sistema avremo:
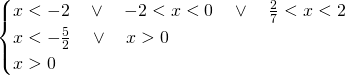
La soluzione sarà quindi:
![]() .
.
(Questa pagina è stata visualizzata da 113 persone)