Se ![]() e
e ![]() sono in progressione aritmetica, qual è il valore di n?
sono in progressione aritmetica, qual è il valore di n?
Affinchè siano in progressione aritmetica, la differenza tra due termini consecutivi deve essere costante; si deve avere, quindi:
![]()
Sviluppiamo i coefficienti binomiali:
![]()
![]()
![]() .
.
Si ha:
![]()
Dividendo per n (sapendo per certo che sia diverso da 0), e facendo il mcm otteniamo:
![]()
![]()
![]()
Quindi avremo due soluzioni:
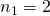 non accettabile
non accettabile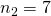 accettabile.
accettabile.
Altri esercizi simili
- Quesito 1 PNI 2010
- Quesito 2 PNI 2010
- Quesito 3 PNI 2010
- Quesito 4 PNI 2010
- Quesito 5 PNI 2010
- Quesito 6 PNI 2010
- Quesito 7 PNI 2010
- Quesito 8 PNI 2010
- Quesito 9 PNI 2010
- Quesito 10 PNI 2010
(Questa pagina è stata visualizzata da 7 persone)