Si consideri la regione delimitata da ![]() , dall’asse x e dalla retta
, dall’asse x e dalla retta ![]() .
.
L’integrale ![]() fornisce il volume del solido:
fornisce il volume del solido:
a) generato da R nella rotazione intorno all’asse x;
b) generato da R nella rotazione intorno all’asse y;
c) di base R le cui sezioni con piani perpendicolari all’asse x sono semicerchi di raggio ![]() ;
;
d) nessuno di questi.
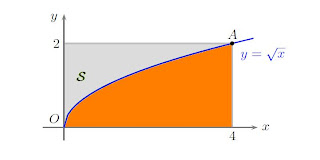
L’area R descritta nell’esercizio è quella che si può vedere in arancio nella figura qui sotto.
Andiamo ad analizzare una per una le possibili soluzioni all’integrale
![]()
1) non può essere questa la soluzione giusta in quanto l’integrale generato da R nella rotazione attorno all’asse x è:
![]()
sia la forma che il valore (di cui si lascia il calcolo) ci dicono che la soluzione è errata.
2) non sembra essere neanche questa la soluzione giusta in quanto l’integrale generato da R nella rotazione attorno all’asse y è:
![]()
ed appare diverso dalla forma che ci è stata presentata, ma se li si vanno a calcolare entrambi si scopre che questi sono equivalenti!!!
3) non può essere neanche questa la soluzione giusta in quanto l’integrale in questa opzione è:
![]()
sia la forma che il valore (di cui si lascia il calcolo) ci dicono che la soluzione è errata.
4) essendo valida la risposta (2), questo esclude di fatto la risposta (4).
Altri esercizi simili
- Quesito 1 PNI 2010
- Quesito 2 PNI 2010
- Quesito 3 PNI 2010
- Quesito 4 PNI 2010
- Quesito 5 PNI 2010
- Quesito 6 PNI 2010
- Quesito 7 PNI 2010
- Quesito 8 PNI 2010
- Quesito 9 PNI 2010
- Quesito 10 PNI 2010
(Questa pagina è stata visualizzata da 6 persone)