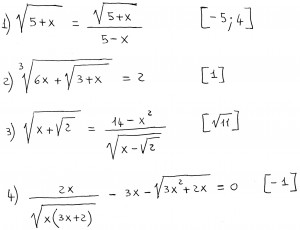Oggetto: Equazioni irrazionali
![]()
![]()
![]()
Quindi avremo due possibilità per la legge di annullamento del prodotto:
Sono ambedue accettabili perchè le condizioni di esistenza impongono che ![]() .
.
Elevando tutto al cubo otteniamo:
![]()
![]()
Eleviamo tutto al quadrato, con la condizione di esistenza che ![]() , ottenendo:
, ottenendo:
![]()
![]()
Senza fare grossi calcoli ci accorgiamo che:
![]()
![]()
![]()
Quindi avremo due possibilità per la legge di annullamento del prodotto:
La prima è accettabile, la seconda no… Si può fare la verifica sostituendo al posto dell’incognita il valore trovato.
Imponendo la condizione di esistenza ![]() , otteniamo:
, otteniamo:
![]()
![]()
Elevando tutto al quadrato, imponendo la condizione di esistenza
![]()
aggiungendo anche che
![]()
otteniamo:
![]()
![]()
Senza fare grossi calcoli ci accorgiamo che:
![]()
![]()
![]()
Avremo due casi:
![]()
ma questa non ammetterà soluzioni accettabili…
![]()
da cui:
![]() è l’unica soluzione accettabile.
è l’unica soluzione accettabile.
Imponendo la condizione di esistenza ![]() otteniamo:
otteniamo:
![]()
![]()
Sapendo che ![]() , otteniamo:
, otteniamo:
![]()
Elevando al quadrato avremo:
![]()
![]()
![]()
da cui
![]() .
.
(Questa pagina è stata visualizzata da 108 persone)