Oggetto: esercizio sulla retta
Corpo del messaggio:
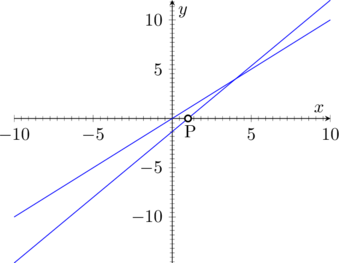
Qual ´e l’equazione della retta passante per il punto
P(1, 0) che nel primo quadrante forma con l’asse delle
ascisse e la retta y = x un triangolo di area 2?
risultato: 4x − 3y − 4 = 0
Potreste farmi vedere come risolverlo?
Calcoliamo innanzitutto la generica retta ![]() passante per il punto P:
passante per il punto P:
![]()
Quindi la retta sarà:
![]()
.
Il terzo vertice del triangolo sarà dato dall’intersezione tra la retta r e la retta ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{cases} y=x \\ y=mx-m\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-17cc8288908da58ebdf6a3f8c6c49250_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=x \\ x=mx-m\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-74b0087ee92694a5fa12056adf3253bf_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=x \\ mx-x=m\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-fa5486f81ea20b90ea8d2f5733709ad9_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} y=\frac {m}{m-1} \\ x=\frac {m}{m-1}\end{cases}\]](http://www.matebook.it/wp-content/ql-cache/quicklatex.com-8dcf4c8d436aca2e18f558867a893e81_l3.png)
I 3 punti del triangolo saranno:
![]()
Vedendo come sarà formato il triangolo, l’area sarà:
![]()
![]()
![]()
![]()
![]()
La retta richiesta sarà quindi:
![]()
facendo il minimo comune multiplo:
![]()
(Questa pagina è stata visualizzata da 104 persone)