Valeria scrive: Equazione con valore assoluto

Pubblicato il da Lo Staff3 commenti
0

Oggetto: equazioni irrazionzali con valore assoluto

Corpo del messaggio:
ciao…come si risolve questo esercizio!!!!Grazie

DSC01175

 

 

    \[\frac {\sqrt {\left|x\right| -5}}{x-1}<3\]

    \[\frac {\sqrt {\left|x\right| -5}}{x-1}-3<0\]

    \[\frac {\sqrt {\left|x\right| -5}-3(x-1)}{x-1}<0\]

Analizziamo separatamente numeratore e denominatore, ponendo entrambi maggiori di 0.

Per il denominatore il discorso è immediato, mentre per il numeratore bisogna fare due calcoli:

    \[\sqrt {\left|x\right| -5}-3(x-1)>0\]

    \[\sqrt {\left|x\right| -5}>3(x-1)\]

Essendoci un valore assoluto, notiamo subito che, per -5<x<5 la disequazione perderebbe di significato, quindi, analizzando gli altri due casi avremmo:

    \[\begin{cases} x \geq 5 \\ \sqrt {x -5}>3(x-1)\end{cases} \quad \quad \begin{cases} x \leq -5 \\ \sqrt {-x -5}>3(x-1)\end{cases}\]

Notiamo subito che, sebbene dovessimo dividere in 2 ambo i sistemi, le condizioni del valore assoluto limitano di per se i calcoli:

    \[\begin{cases} x \geq 5 \\ x -5>9(x^2-2x+1)\end{cases} \quad \quad \begin{cases} x \leq -5 \\ \mbox{indeterminata} \end{cases}\]

    \[\begin{cases} x \geq 5 \\ 9x^2-18x+9-x+5<0\end{cases} \quad \quad \begin{cases} x \leq -5 \\ \mbox{indeterminata} \end{cases}\]

    \[\begin{cases} x \geq 5 \\ 9x^2-19x+14<0\end{cases} \quad \quad \begin{cases} x \leq -5 \\ \mbox{indeterminata} \end{cases}\]

    \[\begin{cases} x \geq 5 \\ \mbox { impossibile }\end{cases} \quad \quad \begin{cases} x \leq -5 \\ \mbox{indeterminata} \end{cases}\]

Andando a mettere in grafico la situazione, ed escludendo tutte le eventuali soluzioni che rimarrebbero nell’intervallo tra -5 e 5, notiamo che la disequazione è sempre verificata per

    \[x \leq -5 \quad \lor \quad x \geq 5\]

 

 

 

 

(Questa pagina è stata visualizzata da 237 persone)

3 pensieri riguardo “Valeria scrive: Equazione con valore assoluto”

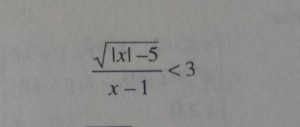
  1. Nel secondo sistema dove sta scritto indeterminata non dovrebbe essere impossibile dato che, andando a svolgere i calcoli, viene

    9x^2-17x+14<0 ed il delta è negativo.

    Poi non mi è chiara la procedura con cui si è giunti alla soluzione finale: se la disequazione del primo sistema è impossibile vuol dire che non ammette soluzioni, quindi il primo sistema dovrebbe essere vuoto. Dunque la soluzione finale dovrebbe uscire solo dal secondo sistema.

    Grazie

  2. Per quanto riguarda la prima domanda, come vedi i due sistemi vengono svolti parallelamente, e quindi la disequazione che vedi è impossibile.

    Per quanto riguarda la soluzione finale, devi considerare, oltre alle soluzioni del sistema, la positività del denominatore discussa precedentemente.
    Quindi, se nel primo sistema, per x maggiore o uguale a 5, notiamo che il numeratore è sempre negativo, il denominatore è sempre positivo, e quindi verifica la disequazione iniziale.
    Nel secondo sistema, il numeratore, per x minore o uguale a 5, il numeratore sarà sempre positivo mentre il denominatore sarà sempre negativo.

    La soluzione finale esce come unione delle due soluzioni.

    Spero di essere stato chiaro.

Lascia un commento