Oggetto: disequazioni irrazionali
Avendo una radice quadrata minore di un polinomio avremo necessità di lavorare solo su un sistema, imponendo determinate condizioni:
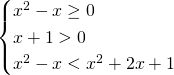
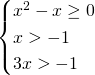
Senza bisogno di fare grossi calcoli possiamo direttamente dire che la prima e la terza disequazione sono verificate per
![]()
![]()
Unendo
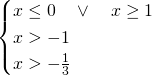
Mettendo a sistema le soluzioni, otterremo subito che la soluzione sarà:
![]()
.
Verifichiamo subito le condizioni di esistenza, e quindi avremo:
![Rendered by QuickLaTeX.com \[\begin{cases} 1-x \geq 0 \\ 1+x \geq 0\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-b6287ac7c3c8c207c6bd7c7e62911a58_l3.png)
![Rendered by QuickLaTeX.com \[\begin{cases} x \leq 1 \\ x \geq -1\end{cases}\]](https://www.matebook.it/wp-content/ql-cache/quicklatex.com-1b0291f3e4ec7e013283429688a40e12_l3.png)
Quindi, se ammette soluzioni, queste devono essere in ![]() .
.
Eleviamo tutto al quadrato ottenendo:
![]()
![]()
![]()
![]()
Intersecando questa soluzione con le condizioni di esistenza, otteniamo:
![]()
(Questa pagina è stata visualizzata da 124 persone)
