Oggetto:
Corpo del messaggio:
![]()
Dominio:
![]()
![]()
![]()
![]() .
.
Studiamo eventuali simmetrie:
![]()
![]()
Quindi la funzione non è ne pari ne dispari.
Studiamo le intersezioni con l’asse delle ascisse, visto che dal dominio escludiamo ogni intersezione con l’asse delle ordinate.
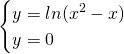
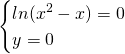
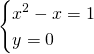
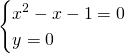
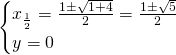
Studiamo la positività della funzione, che, avendo studiato le intersezioni risulta abbastanza semplice, e quindi:
![]()
![]()
![]() .
.
Calcoliamo i limiti negli estremi del dominio:
![]()
![]()
![]()
Non ci sono asintoti obliqui perchè:
![]()
Calcoliamo la derivata prima:
![]()
Studiamo la positività della derivata prima ricordando che, nel dominio, il denominatore è sempre positivo; quindi :
![]() .
.
Da qui avremo che:
![]()
![]()
Non ammetterà punti di massimo o di minimo.
Calcoliamo la derivata seconda:
![]()
Studiamo la positività della derivata prima ricordando che, nel dominio, il denominatore non sarà mai uguale a 0, quindi:
![]()
Ma il ![]() è negativo e quindi la disequazione non è mai verificata, e quindi in ogni intervallo del dominio la funzione avrà la concavità verso il basso.
è negativo e quindi la disequazione non è mai verificata, e quindi in ogni intervallo del dominio la funzione avrà la concavità verso il basso.
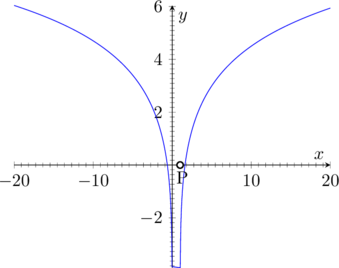
Ecco il grafico:
(Questa pagina è stata visualizzata da 136 persone)