Susanna scrive: Equazioni secondo grado

Pubblicato il 2 Gennaio 2014 da Lo StaffLascia un commento

Oggetto: Equazioni secondo grado

Corpo del messaggio:
Sono solo gli esercizi segnati con il cerchio, ho provato a farli ma i risultati non danno!

Grazie in anticipo

Affinchè l’equazione abbia radice uguale a 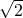$\sqrt 2$ , basterà sostituire questo valore all’incognita e verificare quali siano i valori della a.

$2+\sqrt 2\left(a-2)\sqrt 2+a^2-3a-4=0$

$2+2a-4+a^2-3a-4=0$

$a^2-a-6=0$

$(a-3)(a+2)=0$

$a_1=3$

$a_2=-2$

Nel secondo esercizio, affinchè le due radici siano distinte, deve verificarsi che il delta sia strettamente positivo:

$\Delta >0$

$16m^2-4(2m)(-4m-1)>0$

$16m^2+32m+8m>0$

$48m^2+8m>0$

$m(6m+1)>0$

Avendo l’equazione associata due soluzioni, ed essendo la disequazione maggiore di 0, possiamo subito dire che la disequazione sarà verificata per:

$m<-\frac 16 \quad \lor \quad m>0$

Nel terzo esercizio, affinchè le due radici siano coincidenti, deve verificarsi che il delta sia nullo.

$\Delta=0$

$(1-k)^2-4(k+1)(k-1)=0$

$k^2-2k+1-4k^2+4=0$

$-3k^2-2k+5=0$

$3k^2+2k-5=0$

$k_{\frac 12}=\frac {-2\pm \sqrt {4+60}}{6}=\frac {-2\pm \sqrt {64}}{6}=\frac {-2\pm 8}{6}$

$k_1=-\frac 53$

$k_2=1$

Dobbiamo però escludere la soluzione $k=1$ , in quanto, sostituendola nell’equazione iniziale, questa perderebbe di significato, perchè annullerebbe il coefficiente della $x^2$ .

(Questa pagina è stata visualizzata da 110 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.