Oggetto: Geometria nel piano euclideo

Corpo del messaggio:
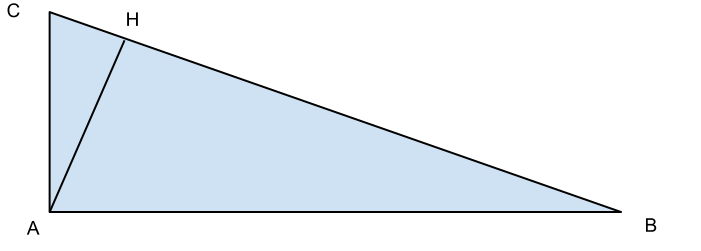
1. Nel triangolo rettangolo ABC traccia l’altezza AH relativa all’ipotenusa BC. Dimostra che i triangoli ABH e ACH sono simili e entrambi sono simili al triangolo dato.

3. Dimostra che la parallela a un lato di un triangolo intersechi i prolungamenti degli altri due lati determina, con il vertice opposto al lato considerato, un triangolo i cui lati sono proporzionali a quelli del triangolo dato.

 

Risposta dello staff

1. Nel triangolo rettangolo iniziale, sapremo che l’angolo in A è retto. Chiamando con l’angolo in B e con l’angolo in C, possiamo subito affermare che nel triangolo ABH, l’angolo in H è retto per costruzione e, di conseguenza, l’angolo BAH sarà proprio .

Da ciò ne deriva che il triangolo ABH e ABC sono simili. Come d’altro canto si dimostra similarmente che il triangolo AHC, dove l’angolo in H è retto e l’angolo in A avrà ampiezza uguale a .

3. Sia BDE il triangolo iniziale. Ci serve dimostrare che ABC sia simile a BDE. Senza grossi dubbi, affermiamo subito che gli angoli BED e BCA sono corrispondenti rispetto alle due parallele DE e AC tagliate dalla trasversale BC. Da questo ne conviene che, per differenza di angoli uguali, anche l’angolo BDE è uguale all’angolo BAC. Quindi, i due triangoli sono simili, e i lati dei due triangoli tra loro in proporzione.

(Questa pagina è stata visualizzata da 106 persone)