Oggetto: Dimostrazioni teoremi geometria

Corpo del messaggio:
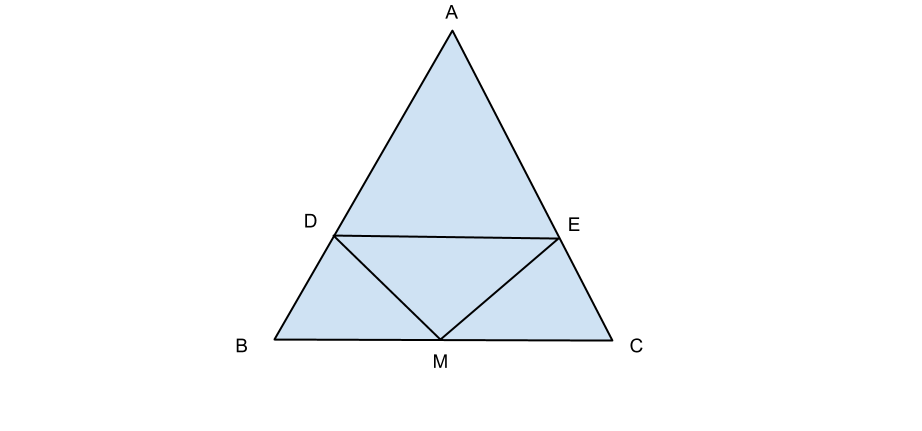
Sia ABC un triangolo isoscele sulla base BC. Sia D un punto di AB ed E un punto di AC tali che AD congruente AE, e sia M il punto medio di BC. Dimostra che MDE è un triangolo isoscele.
Devo usare 1° criterio congruenza dei triangoli e il teorema triangoli isosceli
Grazie, per l’aiuto.

 

Risposta dello staff

Per costruzione sappiamo che

in quanto:

Essendo M il punto medio di BC sappiamo che:

.

Essendo il triangolo ABC isoscele, allora:

Quindi, per il primo criterio di congruenza dei triangoli, avremo che i due triangoli BMD e MCE sono congruenti, avendo due lati e un angolo compreso congruenti.

Di conseguenza a ciò, avremo che:

,

e quindi MDE è isoscele.

 

 

(Questa pagina è stata visualizzata da 267 persone)