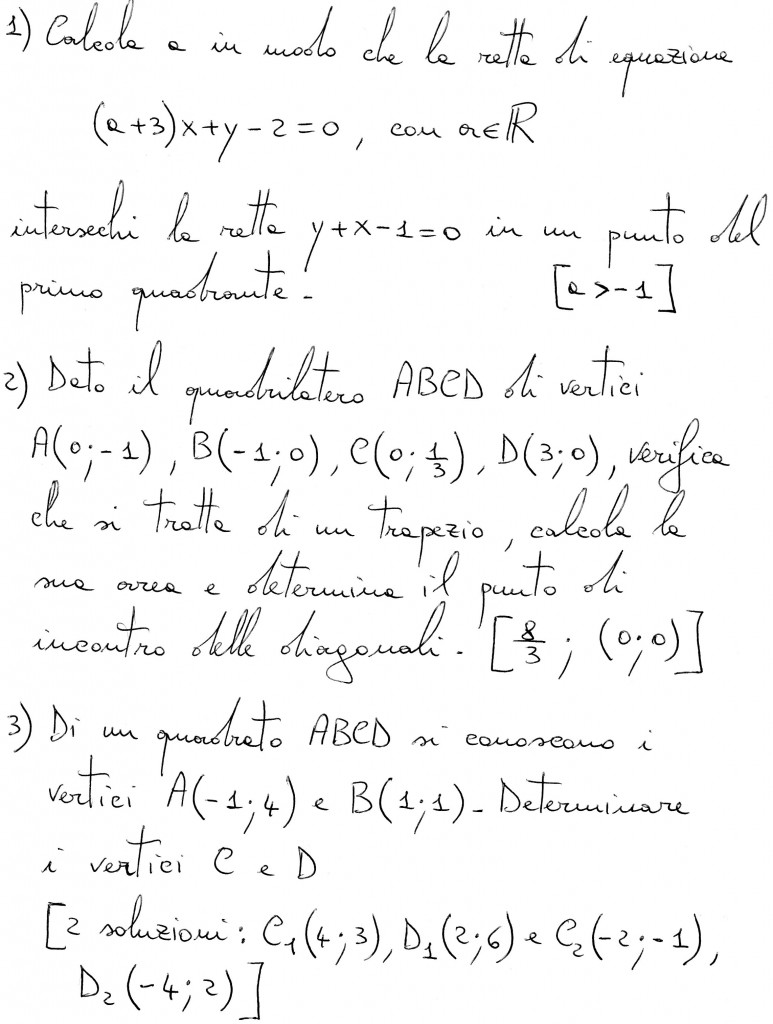Fabio scrive: Problemi sulla retta

Pubblicato il 17 Marzo 2014 da Lo StaffLascia un commento

Oggetto: Problemi sulla retta

Corpo del messaggio:

Risposta dello staff

1) Affinchè le due rette si incontrino in un punto del primo quadrante, deve verificarsi che le coordinate del punto di intersezione siano ambedue positive.

La seconda retta possiamo riscriverla come

$y=1-x$ .

Da qui avremo che, per essere nel primo quadrante, $0<x<1$

Andando a sostituire otteniamo:

$ax+3x+1-x-2=0$

$x(a+2)=1$

$x=\frac {1}{a+2}$

$0<\frac {1}{a+2}<1$

$\begin{cases} \frac {1}{a+2}>0 \\ \frac {1}{a+2}<1 \end{cases}$

$\begin{cases} a>-2 \\ \frac {1-a-2}{a+2}<0\end{cases}$

$\begin{cases} a>-2 \\ \frac {a+1}{a+2}>0\end{cases}$

$\begin{cases} a>-2 \\a<-2 \quad \lor \quad a>-1\end{cases}$

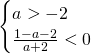
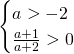
Di conseguenza la soluzione sarà:

$a>-1$ .

2)

Calcoliamo le rette dei lati opposto e verifichiamo che due siano parallele e due no.

$r_{AB}: y=-x-1$

$r_{BC}: y=\frac 13 x+\frac 13$

$r_{CD}: y=-\frac 19x+\frac 13$

$r_{AD}: y=\frac 13 x-1$

Come ci aspettavamo AD e BC sono paralleli.

Per calcolare l’altezza del trapezio usiamo la formula della distanza punto-retta di B dalla retta di AD riscrivendola in maniera esplicita:

$r_{AD}: x-3y-3=0$

$h=\frac { \left| -1-0-3 \right|}{\sqrt{1+9}}=\frac {4}{\sqrt {10}}=\frac 25 \sqrt {10}$

Calcoliamo ora la lunghezza delle due basi:

$AD= \sqrt{(0-3)^2+(-1-0)^2}=\sqrt{10}$

$BC= \sqrt{(-1-0)^2+(0-\frac 13)^2}=\sqrt{1+\frac 19}=\frac {\sqrt{10}}{3}$

$A_{ABCD}=\frac {(AB+CD) \cdot h}{2}=\frac {\frac 43 \sqrt{10} \cdot \frac 25 \sqrt{10}}{2}=\frac 83$

Per calcolare il punto di intersezione delle diagonali, non serve fare grossi calcoli, visto che le loro rette saranno:

$r_{AC}: y=0$

$r_{BD}: x=0$

Di conseguenza l’origine sarà il punto di intersezione delle diagonali.

3)

Calcoliamo la lunghezza del lato del quadrato:

$AB=\sqrt {(-1-1)^2+(4-1)^2}=\sqrt {4+9}=\sqrt{13}$

Calcoliamo la retta che passa per A e B:

$r: \frac {y-4}{1-4}=\frac {x+1}{1+1}$

$2y-8=-3x-3$

$3x+2y-5=0$

Da qui troviamo le due rette perpendicolari a questa passanti per i due punti:

$s_A: 2x-3y+q=0$

Da cui:

$s_A: 2x-3y+14=0$

$s_B: 2x-3y+q=0$

Da cui:

$s_B: 2x-3y+1=0$ .

Ora dobbiamo trovare i punti di queste rette che hanno distanza uguale alla lunghezza del lato:

I punti C e D avranno coordinate:

$D\left(x;\frac 23x+\frac {14}{3}\right)$

$C\left(x;\frac 23x+\frac {1}{3}\right)$

$BC=\sqrt{(1-x)^2+\left(1-\frac 23x-\frac {1}{3}\right)^2$

$BC=\sqrt{(1-x)^2+\left(\frac 23-\frac 23x\right)^2$

Elevando tutto al quadrato otteniamo:

$1-2x+x^2+\frac 49x^2-\frac {8}{9}x+\frac {4}{9}=13$

$9-18x+9x^2+ 4x^2 -8x+4-117=0$

$13x^2 -26x-104=0$

$x^2-2x-8=0$

$(x-4)(x+2)=0$

Quindi, ammetterà la possibile esistenza di due punti C di coordinate:

$C_1(4;3)$

$C_2(-2;-1)$ .

Calcoliamo le coordinate di D nello stesso modo ma utilizzano l’altra retta:

$AD=\sqrt{(-1-x)^2+\left(4-\frac 23x-\frac {14}{3}\right)^2$

$AD=\sqrt{(-1-x)^2+\left(-\frac 23-\frac 23x\right)^2$

Elevando tutto al quadrato otteniamo:

$1+2x+x^2+\frac 49x^2+\frac {8}{9}x+\frac {4}{9}=13$

$9+18x+9x^2+ 4x^2 +8x+4-117=0$

$13x^2 +26x-104=0$

$x^2+2x-8=0$

$(x+4)(x-2)=0$

Quindi, ammetterà la possibile esistenza di due punti C di coordinate:

$D_1(2;6)$

$D_2(-4;-2)$ .

(Questa pagina è stata visualizzata da 71 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.