Oggetto: Problemi sull’iperbole
Corpo del messaggio:
Sono i problemi segnati con la matita nel libro 
Risposta dello staff
196)
a) Data l’equazione ![]() ,la lunghezza del semiasse trasverso sarà:
,la lunghezza del semiasse trasverso sarà: ![]() .
.
Di conseguenza avremo che:
![]()
![]()
![]()
b) FAI IL GRAFICO
c)
I vertici saranno:
![]()
![]()
I fuochi saranno:
![]()
![]()
d)
Visto che i vertici giacciono su ![]() , allora le tangenti passante per i vertici saranno parallele di
, allora le tangenti passante per i vertici saranno parallele di ![]()
Avremo quindi:
![]()
![]()
Le due rette saranno quindi:
![]()
197)
Affinchè siano tangenti alla circonferenza nei vertici, bisogna considerare i punti della circonferenza tali per cui ![]() . Di conseguenza avremo:
. Di conseguenza avremo:
![]()
![]()
![]() .
.
Quindi, se la circonferenza è tangente nei punti ![]() avremo che l’iperbole ha equazione
avremo che l’iperbole ha equazione ![]() , se la circonferenza è tangente nei punti
, se la circonferenza è tangente nei punti ![]() avremo che l’iperbole ha equazione
avremo che l’iperbole ha equazione ![]() .
.
I vertici avranno coordinate
![]()
![]()
![]()
![]()
Si capisce subito che è un quadrato e la sua area sarà:
![]()
198)
Mettendo a sistema retta ed iperbole generica otteniamo:
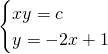
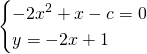
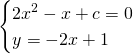
![]()
Di conseguenza i due punti avranno coordinate:
![]()
![]()
Calcoliamo la distanza tra A e B e poniamola uguale alla richiesta dell’esercizio:
![]()
![]()
![]()
![]()
![]()
![]()
L’equazione dell’iperbole sarà: ![]()
(Questa pagina è stata visualizzata da 70 persone)