Oggetto: Fasci di rette
Corpo del messaggio:
a)
Le due rette generatrici saranno:
e 
Il centro del fascio sarà:
Per capire il verso, basta trovare il valore di k per il passaggio della retta per l’origine. Sapendo che, per 
, avremo , ed essendo, in questo caso, 
, allora il senso sarà orario all’aumentare di k.
b) 
Le due rette generatrici saranno:
e 
.
Il centro del fascio sarà:
Per capire il verso, basta trovare il valore di k per il passaggio della retta per l’origine. Sapendo che, per , avremo , ed essendo, in questo caso, 
, allora il senso sarà antiorario all’aumentare di k.
c)
Le due rette generatrici saranno:
e 
Il centro del fascio sarà, sviluppando il sistema:
Troviamo 2 punti particolari per capire il valore di k; se passa per l’origine, avremo 
. Se passa per il punto (3;0), avremo 
. Di conseguenza il senso sarà antiorario.
d)
Le due rette generatrici saranno:
e 
Il centro del fascio sarà:
Per capire il verso, basta trovare il valore di k per il passaggio della retta per un particolare punto, in questo caso (-1,0). Sapendo che, per , avremo , ed essendo, in questo caso, , allora il senso sarà antiorario all’aumentare di k.
e)
Questo sarà un fascio improprio in quanto, dividendo tutto per k, ipotizzando che questo sia diverso da 0 otteniamo:
ovvero un fascio di rette parallele!!!
(Questa pagina è stata visualizzata da 310 persone)
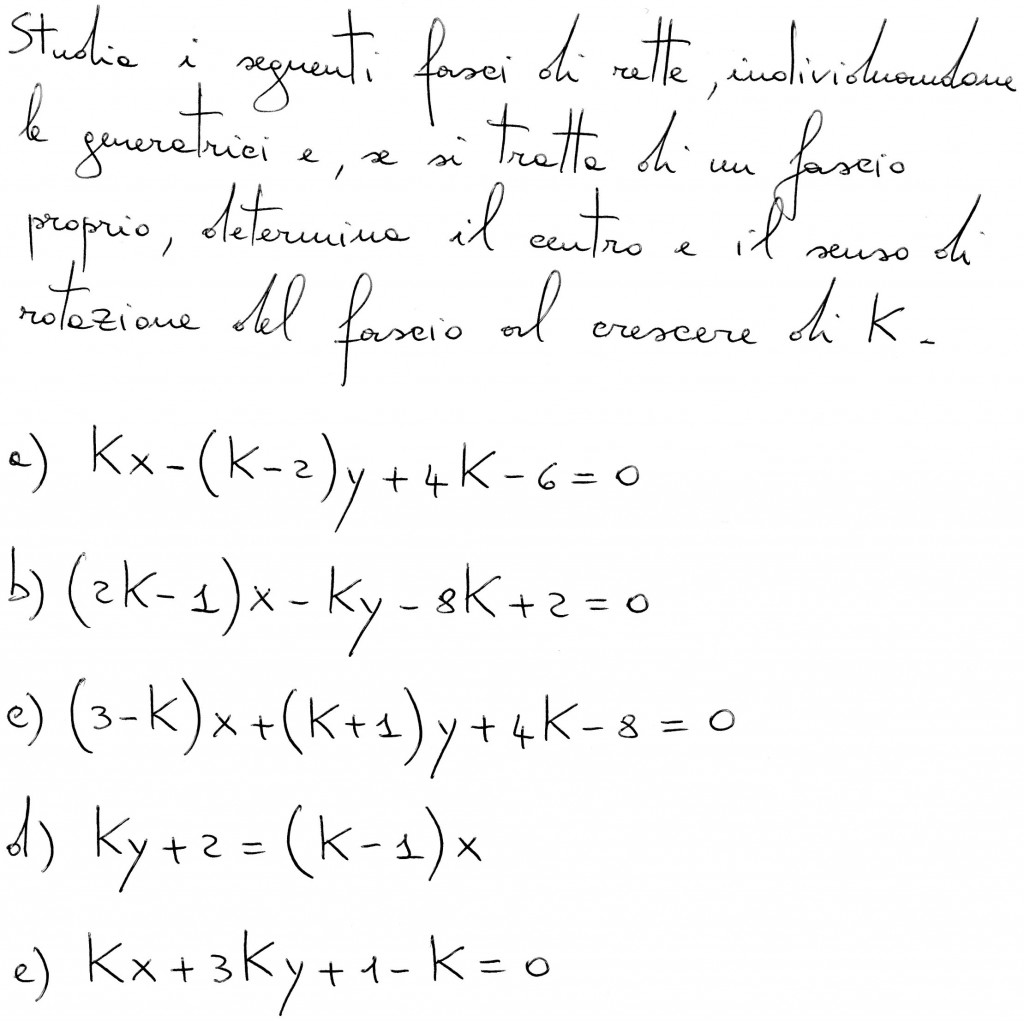
Spett.le Prof., vorrei un chiarimento su come si determina il senso di rotazione delle rette.
In pratica bisogna assegnare un valore a piacere a k e rappresentare la retta corrispondente e vedere come ruotano.
In merito all’esercizio a)ad esempio, per k=0 ottengo la retta y=3; per k=1 ottengo la retta y= – x+2 e poi per k che tende all’infinito ottengo la retta esclusa dal fascio cioè y = x+4. Ora andando a rappresentarle graficamente si nota che al crescere di k, le rette ruotano in senso orario e non in senso antiorario come scritto da Lei.
In merito all’esercizio b) per k= 0 ottengo la retta x=2; per k=1 ottengo la retta y=x-6 e poi per k che tende all’infinito si ha y = 2x-8. Andando a rappresentarle, all’aumentare di k si osserva che la retta per k = 0 raggiunge la retta per k=1 senza sovrapporsi alla retta esclusa del fascio ruotando in senso antiorario e non orario come da lei scritto.
Anche per l’esercizio c) ripetendo la pocedura illustrata mi ritrovo che le rette ruotano in senso antiorario e non orario.
Vorrei sapere se il mio ragionamento è corretto oppure no, e se non lo fosse gradirei un maggiore chiarimento su come si determina il senso di rotazione.
La ringrazio anticipatamente.
Per quanto riguarda i 3 esercizi hai ragione tu… ho descritto il procedimento giusto (che d’altronde hai seguito pure tu), ma ho scritto i versi opposti. Errore di distrazione riveduto e corretto.