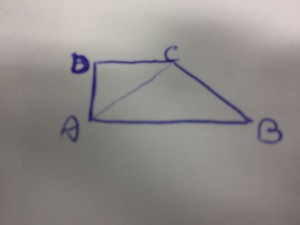
Soluzione e svolgimento del seguente problemi di geometria piana.
- Determinare le lunghezze dei lati di un trapezio rettangolo, di area
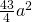 , sapendo che la diagonale minore è lunga 5a e che l’altezza supera di a la base minore.
, sapendo che la diagonale minore è lunga 5a e che l’altezza supera di a la base minore.
Dai dati otteniamo che:
![]()
![]()
![]()
Chiamiamo ![]() , e sfruttiamo il teorema di Pitagora sul triangolo
, e sfruttiamo il teorema di Pitagora sul triangolo ![]() . Otterremo:
. Otterremo:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (non accettabile perchè negativo…)
(non accettabile perchè negativo…)
Quindi:
![]()
![]()
Per trovare ![]() sfruttiamo la conoscenza dell’area del trapezio, ottenendo:
sfruttiamo la conoscenza dell’area del trapezio, ottenendo:
![]()
Chiamando ![]() , otteniamo
, otteniamo
![]()
![]() (moltiplicando per 4 e dividendo per
(moltiplicando per 4 e dividendo per ![]() ):
):
![]()
Altri esercizi simili:
- Esercizi equazioni di secondo grado: Problema 1 di geometria piana
- Esercizi equazioni di secondo grado: Problema 2 di geometria piana
- Esercizi equazioni di secondo grado: Problema 3 di geometria piana
- Esercizi equazioni di secondo grado: Problema 4 di geometria piana
- Esercizi equazioni di secondo grado: Problema 5 di geometria piana
- Esercizi equazioni di secondo grado: Problema 6 di geometria piana
- Esercizi equazioni di secondo grado: Problema 7 di geometria piana
- Esercizi equazioni di secondo grado: Problema 8 di geometria piana
- Esercizi equazioni di secondo grado: Problema 9 di geometria piana
- Esercizi equazioni di secondo grado: Problema 10 di geometria piana
- Esercizi equazioni di secondo grado: Problema 11 di geometria piana
- Esercizi equazioni di secondo grado: Problema 12 di geometria piana
(Questa pagina è stata visualizzata da 732 persone)