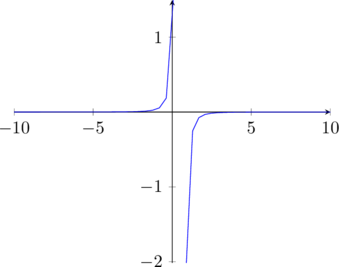
Oggetto: trovare le coordinate dei massimi e dei minimi,le intersezioni con gli assi ed eventuali asintoti +grafico
Corpo del messaggio:
Salve,potreste aiutarmi a risolvere questo esercizio? Grazie in anticipo 🙂
![]()
Risposta dello staff
- Insieme di definizione
Essendo una funzione razionale fratta, imponiamo che il denominatore sia diverso da 0 e quindi il dominio sarà: ![]() .
.
- Simmetrie e periodicità
![]()
![]()
Questa funzione non avrà simmetrie.
- Intersezioni con gli assi
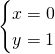
Non avrà intersezioni con l’asse delle x.
La funzione, quindi, avrà una sola intersezione con gli assi:
![]() .
.
- Segno della funzione
Studiamo la positività di ![]() :
:
![]()
![]()
![]()
- condizione agli estremi
![]()
![]() è anche asintoto orizzontale.
è anche asintoto orizzontale.
- Asintoti
![]()
![]()
![]() è un asintoto verticale.
è un asintoto verticale.
- Studio della derivata prima
![]()
![]()
Dato che questa disequazione è sempre verificata, ![]() , avremo che la funzione sarà crescente nei due intervalli:
, avremo che la funzione sarà crescente nei due intervalli:
![]() e
e ![]()
Non annullandosi mai la derivata prima questa funzione non avrà ne massimi ne minimi.
(Questa pagina è stata visualizzata da 109 persone)