Luca scrive: Funzione

Oggetto: Funzione

Corpo del messaggio:
Data la funzione:

f(x)=x^2[1+sen(1/x)] se x diverso da 0, f(0)=0

1) Studiare continuità e derivabilità di f nel suo dominio
2) Esiste un valore massimo assunto da f? Esiste un valore minimo assunto da f?
3) é vero che f(x)>0 in un opportuno intorno dell’origine delle coordinate?
e l’altro è:

Si consideri la funzione f(x)= (1+|lnx|)/(1+lnx)
1) dire dominio di f
2)dopo aver studiato la positività, calcolare i limiti agli estremi.
3)Calcolare,se esistono, f'(1),f'(4) (f’ denota la derivata di f)
4) Dire se esistono a>1 t.c. integrale definito dove a= 1 e b=a di (f(x)dx=0)

Risposta dello staff

$f(x)=x^2\left[1+sen(\frac 1x ) \right]$

1) Il dominio della funzione è $\mathbb{R}$ .

Per studiare la continuità, ci basta studiare cosa succede per $x=0$ , visto che per tutti gli altri valori, la funzione ha sempre valore:

$\lim_{x \to 0^\pm} x^2\left[1+sen\left(\frac 1x \right) \right] =\lim_{x \to 0^\pm} x^2\left[1+\frac 1x \right] =$

$=\lim_{x \to 0^\pm} x^2+x=0$

Quindi, la funzione è continua anche in 0.

Studiamo la derivabilità:

$f'(x)=2x\left[1+sen(\frac 1x ) \right] +x^2(cos(\frac 1x)\cdot -\frac {1}{x^2})=2x\left[1+sen(\frac 1x ) \right] -cos(\frac 1x)$

Si nota che, a differenza di prima, qui ci sarebbe da calcolare il limite del $cos\left(\frac 1x\right)$ in 0, che, non essendo definito rende la funzione derivabile in tutto R tranne in 0.

2) Un valore massimo questa funzione non lo assumerà mai, in quanto, per $x \to \pm infty$ , $sen \frac 1x \to 0$ e la funzione tenderà a $+\infty$ .

Invece ammetterà valore minimo proprio nell’origine, in quanto la funzione risulta prodotto di due fattori sempre positivi, e di conseguenza il minimo che potrà assumere sarà proprio 0.

3) Senza bisogno di calcoli, la risposta a questa affermazione è data nella risposta precedente.

$f(x)=\frac {1+\left|lnx \right|}{1+lnx}$

1) Per lo studio del dominio dovremo imporre che l’argomento del logaritmo sia sempre strettamente positivo e che il denominatore non sia mai uguale a 0, quindi:

$\begin{cases} x >0 \\ logx \neq -1 \end{cases}$

$\begin{cases} x >0 \\ x \neq e^{-1} \end{cases}$

$\begin{cases} x >0 \\ x \neq \frac 1e \end{cases}$

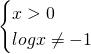
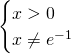
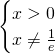
Il dominio sarà quindi:

$]0;\frac 1e[ \quad \cup \quad ]\frac 1e; +\infty[$

2) Per lo studio della positività notiamo che il numeratore è sempre positivo nel dominio, in quanto somma di un numero positivo e di un valore assoluto.

Il denominatore sarà positivo per $x>\frac 1e$ .