Sia ![]()
A lato è disegnato il grafico ![]() di
di ![]() . Si dimostri che
. Si dimostri che ![]() è centro di simmetria di
è centro di simmetria di ![]() e si calcoli, in gradi e primi sessagesimali, l’angolo che la tangente in esso a
e si calcoli, in gradi e primi sessagesimali, l’angolo che la tangente in esso a ![]() forma con la direzione positiva dell’asse x .
forma con la direzione positiva dell’asse x .
Risposta dello staff

Per dimostrare che ![]() è centro di simmetria per
è centro di simmetria per ![]() bisognerà ricavare che la funzione con un nuovo sistema di riferimento risulti dispari. La funzione
bisognerà ricavare che la funzione con un nuovo sistema di riferimento risulti dispari. La funzione ![]() , con la traslazione di assi
, con la traslazione di assi 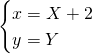 , diventa:
, diventa:
![]()
![]()
![]()
La funzione così ottenuta è dispari, difatti ![]() , perciò il grafico di
, perciò il grafico di ![]() risulta simmetrico rispetto al punto
risulta simmetrico rispetto al punto ![]() .
.
La derivata di ![]() è:
è:
![]()
![]()
L’angolo ![]() formato dalla retta tangente a
formato dalla retta tangente a ![]() in
in ![]() è tale che
è tale che ![]() .
.
Si ha che ![]() , da cui
, da cui ![]()
L’ampiezza dell’angolo formato dalla retta tangente a ![]() in
in ![]() è circa 116°34′ .
è circa 116°34′ .
Altri esercizi simili
(Questa pagina è stata visualizzata da 13 persone)