Oggetto: Disequazione trigonometrica
Corpo del messaggio:
risolvere la disequazione trigonometrica.
Grazie mille
Risposta dello staff
![]()
![]()
![]()
Dividendo tutto per ![]() , e quindi, imponendo che
, e quindi, imponendo che ![]() , con
, con ![]() , otteniamo:
, otteniamo:
![]()
![]()
Chiamando ![]() e
e ![]() i due angoli per i quali la tangente assume il valore considerato avremo il risultato, nell’intervallo
i due angoli per i quali la tangente assume il valore considerato avremo il risultato, nell’intervallo ![]() :
:
![]()
(Questa pagina è stata visualizzata da 200 persone)
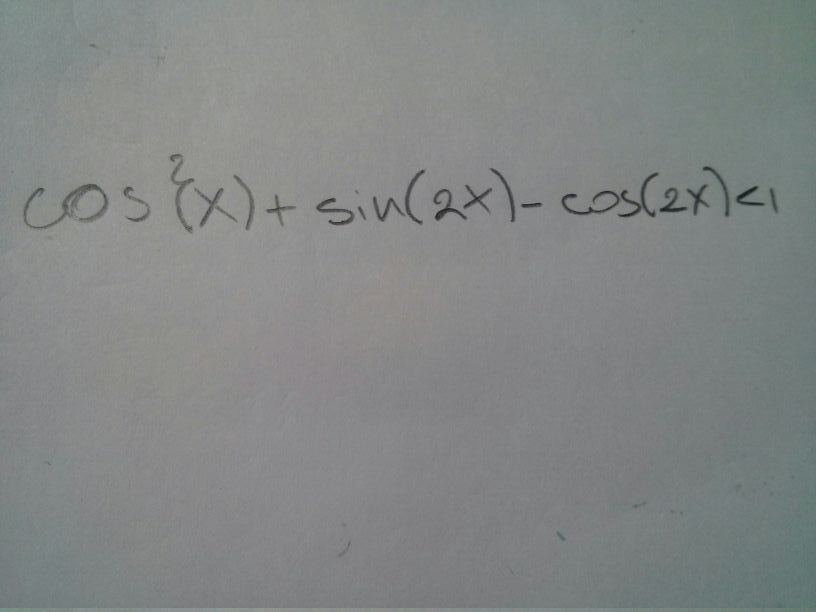
Grazie mille per la soluzione!
Comunque vorrei sapere perché quando pongo x diverso da 1/2 scrivo +kpigreco e non +2kpigreco ?
Innanzitutto mi scuso perchè mi ero dimenticato di scrivere che, nell’intervallo [0;2 pigreco], k può essere uguale solo a 0 e ad 1.
Per la tua domanda, se scrivessi solo “+2kpigreco”, non considererei la possibilità che il coseno si annulli in 3/2 pigreco, ovvero a 270°.
Ok, ho capito! Grazie mille e super efficienti!
Grazie a te!!! 😉