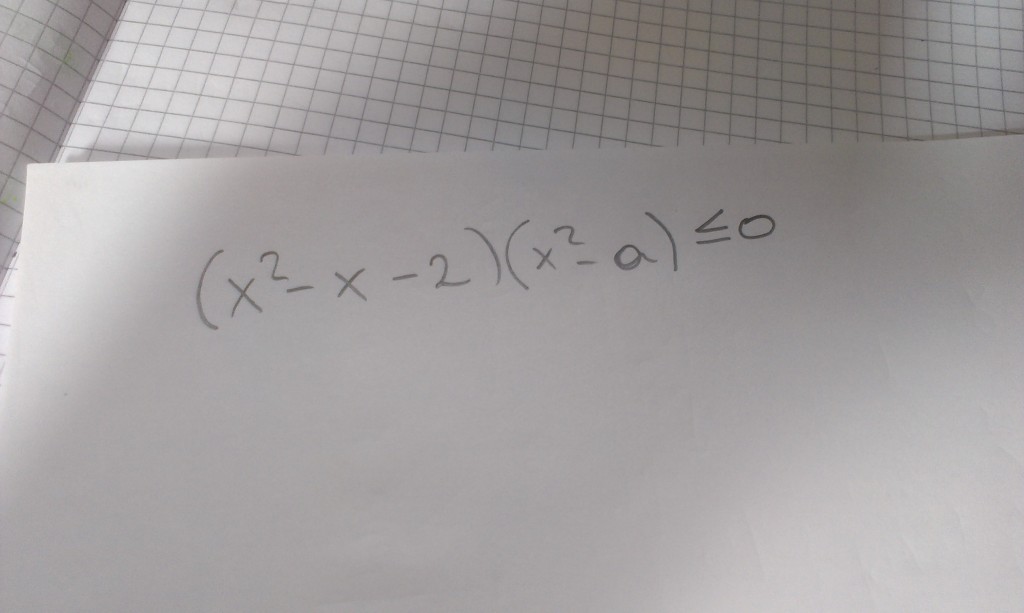Oggetto: Soluzione disequazione parametrica
Corpo del messaggio:
Risposta dello staff
Analizziamo separatamente i due fattori:
![]()
Studiamo l’equazione associata:
![]()
![]()
![]()
![]()
Andando a vedere le soluzioni in questo link, avremo che questa disequazione è verificata per:
![]()
Studiamo il secondo fattore:
![]()
Se ![]() avremo:
avremo:
![]()
da cui:
![]()
Se invece ![]() , l’equazione associata è impossibile e la disequazione sempre verificata.
, l’equazione associata è impossibile e la disequazione sempre verificata.
Quindi, in base al valore di a, avremo diversi risultati:
la disequazione iniziale sarà verificata per
![]() .
.
![]()
![]()
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 64 persone)