Oggetto: Soluzione disequazione parametrica
Corpo del messaggio: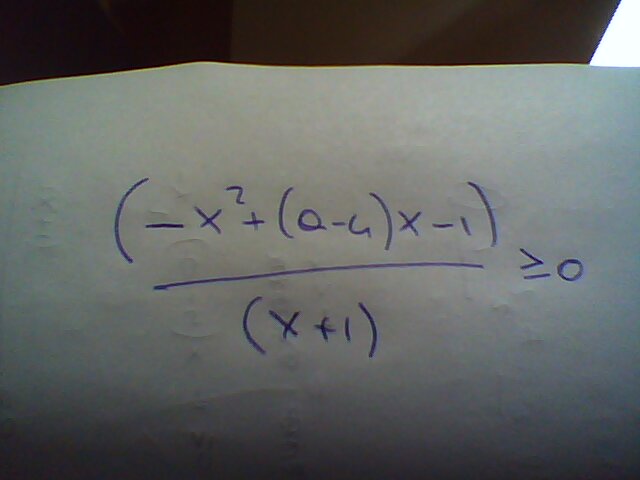
Risposta dello staff
Andiamo a studiare separatamente numeratore e denominatore.
![]()
![]()
Andiamo a risolvere l’equazione associata:
![]()
Quindi avremo che per
![]() , il
, il ![]() sarà negativo e quindi l’equazione non ammette soluzioni.
sarà negativo e quindi l’equazione non ammette soluzioni.
![]() , il
, il ![]() è uguale a 0, e l’equazione ammetterà due soluzioni coincidenti.
è uguale a 0, e l’equazione ammetterà due soluzioni coincidenti.
![]() il
il ![]() sarà positivo e l’equazione ammetterà due soluzioni distinte reali.
sarà positivo e l’equazione ammetterà due soluzioni distinte reali.
Ora, analizziamo le tre casistiche e risolviamo la disequazione principale:
- Se il
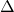 è negativo, allora, la disequazione del numeratore non è mai verificata, e quindi la disequazione principale sarà verificata per
è negativo, allora, la disequazione del numeratore non è mai verificata, e quindi la disequazione principale sarà verificata per 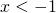
- Se il
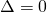 , la disequazione al numeratore non sarà mai verificata eccetto per un valore.
, la disequazione al numeratore non sarà mai verificata eccetto per un valore.
Per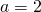 , il numeratore sarà
, il numeratore sarà  , e quindi la disequazione sarà verificata per
, e quindi la disequazione sarà verificata per 
Per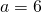 il numeratore sarà
il numeratore sarà  , e quindi la disequazione sarà verificata per
, e quindi la disequazione sarà verificata per 
- Se il
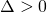 , bisognerà studiare il segno delle soluzioni:
, bisognerà studiare il segno delle soluzioni: e la loro posizione rispetto a -1.
e la loro posizione rispetto a -1.
(Questa pagina è stata visualizzata da 77 persone)