Esercizio 1 Martina

Risolvi la seguente disequazione di secondo grado:

$\left|x^2-1 \right| \geq 4-2x$

Risposta dello staff

Si tratterà di studiare due sistemi, derivanti dalla positività del valore assoluto:

$\begin{cases} x^2-1 \geq 0 \\ x^2-1 \geq 4-2x \end{cases} \quad \quad \begin{cases} x^2-1 < 0 \\ 1-x^2 \geq 4-2x \end{cases}$

$\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x^2-1 +2x-4\geq 0 \end{cases} \quad \quad \begin{cases} -1<x<1 \\ x^2-1-2x+4 \leq 0 \end{cases}$

$\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x^2 +2x-5\geq 0 \end{cases} \quad \quad \begin{cases} -1<x<1 \\ x^2-2x+3 \leq 0 \end{cases}$

$\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x\leq \frac{-2 - 2\sqrt {6}}{2} \quad \lor \quad x\leq \frac{-2 + 2\sqrt {6}}{2} \end{cases} \quad \quad \begin{cases} -1<x<1 \\ \mbox{ impossibile } \end{cases}$

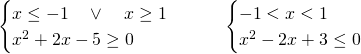
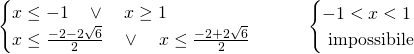
La disequazione iniziale quindi, sarà verificata solo nella soluzione del primo sistema, ovvero:

$x\leq \frac{-2 - 2\sqrt {6}}{2} \quad \lor \quad x \geq 1$ .

(Questa pagina è stata visualizzata da 73 persone)

Matebook

La matematica spiegata passo passo

Esercizio 1 Martina

Risposta dello staff

Un pensiero riguardo “Esercizio 1 Martina”

Lascia un commento Annulla risposta