Michael scrive: svolgimento problema

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: svolgimento problema

Corpo del messaggio:
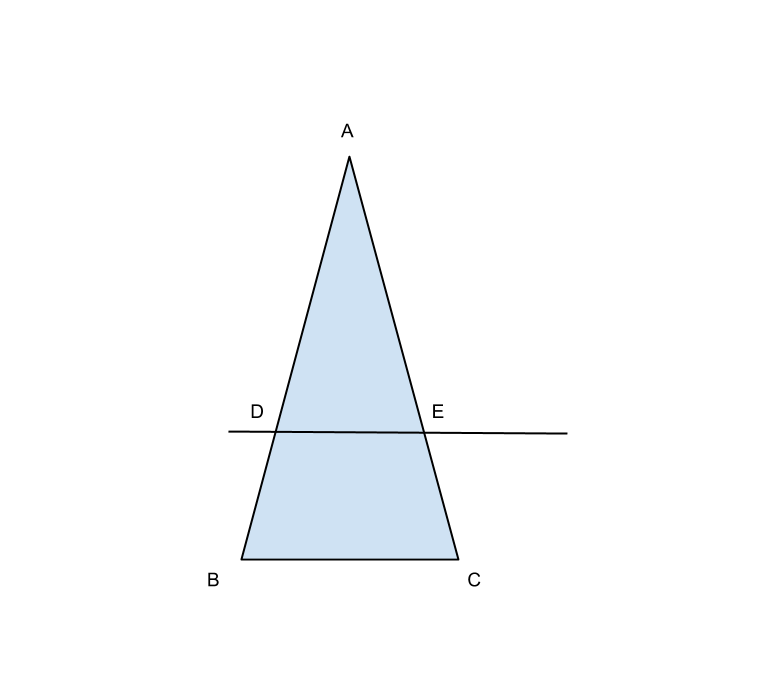
Nel triangolo isoscele ABC la  base e l’altezza a essa relativa misurano rispettivamente 48 cm e 32 cm .sapendo che il segmento DE parallelo alla base e lungo 30 cm calcola il perimetro e l’area del triangolo ADE.

Risposta dello staff

triangolo isoscele con segmento

Dai dati sappiamo che:

BC=48 \mbox{ cm}

l’altezza

AH= 32 \mbox{ cm}

e il segmento

DE= 30 \mbox{ cm}

Ricaviamo subito il lato obliquo del triangolo ABC con il teorema di Pitagora:

AB=AC=\sqrt{AH^2+BH^2}=\sqrt{1024+576} \mbox{ cm}=\sqrt{1600} \mbox{ cm}=40\mbox{ cm}

Il rapporto dei lati dei triangoli sarà dato dal rapporto tra le due basi, essendo i triangoli simili e quindi:

r=\frac {BC}{DE}=\frac {48}{30}=\frac 85

Da qui ricaviamo il lato obliquo del triangolo ADE:

AD=AE=\frac 58 \cdot 40 \mbox{ cm}=25 \mbox{ cm}

L’altezza relativa alla base sarà:

AM=\frac 58 \cdot 32 \mbox{ cm}=20 \mbox{ cm}

Ricaviamo perimetro e area di ADE:

2p=(25+25+30) \mbox{ cm}=80\mbox{ cm}

A=\frac{30 \cdot 25}{2}\mbox{ cm}^2=375\mbox{ cm}^2

(Questa pagina è stata visualizzata da 95 persone)

Lascia un commento