Esercizio svolto sullo studio di funzione: punto d

Data la funzione

$y=a+b\, log_2x$

Dimostra mediante il procedimento di verifica dei limiti che la funzione g(x) presenta un asintoto orizzontale e uno obliquo

Calcoliamo il dominio:

$g(x)=\frac{1}{4-log_2(x)}-1$

$\begin{cases} x>0 \\ 4-log_2(x)\neq 0\end{cases}$

$\begin{cases} x>0 \\ log_2(x)\neq 4\end{cases}$

$\begin{cases} x>0 \\ x\neq 2^4\end{cases}$

$\begin{cases} x>0 \\ x\neq 16\end{cases}$

$D=x>0 \mbox{ con } x \neq 16$

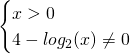
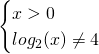
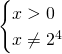
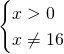
Calcoliamo i limiti negli estremi:

$\lim_{x \to 0^+} g(x)=-1$

$\lim_{x \to 16^-} g(x)=+\infty$

$\lim_{x \to 16^+} g(x)=-\infty$

$\lim_{x \to +\infty} g(x)=-1$

Da questi risultati notiamo che i due asintoti sono:

$x=16$ asintoto verticale e

$y=-1$ asintoto orizzontale.

(Questa pagina è stata visualizzata da 89 persone)

Matebook