![]()
Risposta dello staff
Calcoliamo il dominio:
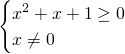
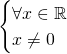
![]()
Calcoliamo la positività, notando che, il numeratore è strettamente positivo e quindi:
![]()
![]()
![]()
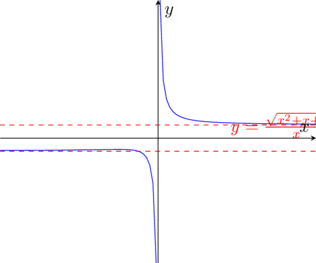
Calcoliamo i limiti negli estremi del dominio:
![]()
![]()
![]()
Calcoliamo la derivata prima:
![]()
![]()
![]()
Studiamo la positività della derivata prima notando che il denominatore è sempre positivo ![]() e quindi:
e quindi:
![]()
![]()
![]()
(Questa pagina è stata visualizzata da 50 persone)