Lucrezia scrive: problema di secondo grado

Pubblicato il da Lo StaffLascia un commento
-2

Oggetto: problema di secondo grado

Corpo del messaggio:
un quadrato ha perimetro 24 cm. un rettangolo ha lo stesso perimetro, mentre l’area è pari ai 3/4 di quella del quadrato. determina le dimensioni del rettangolo

Risposta dello staff

Chiamando con l il lato del quadrato, ricaviamo subito la sua area:

l=\frac 14 24 \mbox{ cm}=6\mbox{ cm}

A_Q=6 \cdot 6 \mbox{ cm}^2=36 \mbox{ cm}^2

Da qui ricaviamo l’area del rettangolo:

A_R=\frac 34 36 \mbox{ cm}^2=27\mbox{ cm}^2

Risolviamo il sistema per ricavare le dimensioni del rettangolo:

\begin{cases} 2x+2y=24 \\ xy=27\end{cases}

\begin{cases} x+y=12 \\ xy=27\end{cases}

\begin{cases} x=12-y \\ xy=27\end{cases}

\begin{cases} x=12-y \\ (12-y)y=27\end{cases}

\begin{cases} x=12-y \\ 12y-y^2=27\end{cases}

\begin{cases} x=12-y \\ y^2-12y+27=0\end{cases}

\begin{cases} x=12-y \\ (y-9)(y-3)=0\end{cases}

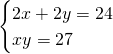
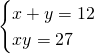
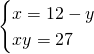
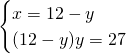
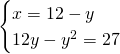
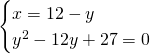
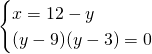
I due lati avranno dimensioni 3 e 9 cm.

(Questa pagina è stata visualizzata da 76 persone)

Lascia un commento