Problemi di primo grado 4

-1

Determinare due numeri sapendo che il maggiore supera di 8 i \frac 34 del minore e che la somma di \frac 15 del maggiore e dei \frac 38 del minore è 10. (20, 16)

\Bigg\{ \begin{array}{l} x=\frac34 y +8 \\ \frac 15 x+ \frac 3 8 y=10 \end{array}

\Bigg\{ \begin{array}{l} \frac {4x -3y}4= \frac {32}4 \\ \frac {8x+15y}{40}=\frac {400}{40} \end{array}

\Bigg\{ \begin{array}{l} 4x -3y= 32 \\ 8x+15y=400 \end{array}

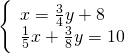
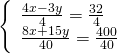
Moltiplicando per 2 la prima equazione otteniamo per la x lo stesso coefficiente… a quel punto basta fare sottrarre la prima alla seconda.

\Bigg\{ \begin{array}{l} 8x -6y= 64 \\ 8x+15y=400 \end{array}

\Bigg\{ \begin{array}{l} 4x -3y= 32 \\ 15y-(-6y)=400-64 \end{array}

\Bigg\{ \begin{array}{l} 4x = 32+3y \\ 21y=336 \end{array}

\Bigg\{ \begin{array}{l} x = \frac {32+3y}4 \\ y=16 \end{array}

\Bigg\{ \begin{array}{l} x = \frac {32+3\cdot 16}4 \\ y=16 \end{array}

\Bigg\{ \begin{array}{l} x = \frac {32+48}4 \\ y=16 \end{array}

\Bigg\{ \begin{array}{l} x = \frac {80}4 \\ y=16 \end{array}

\Bigg\{ \begin{array}{l} x = 20 \\ y=16 \end{array}

 

 

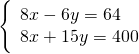
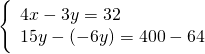
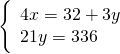
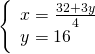
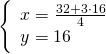
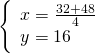
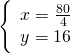
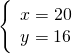
Altri hanno visualizzato:

(Questa pagina è stata visualizzata da 288 persone)

Lascia un commento