Problema 5 di geometria con due o più incognite

0

 

Risoluzione e spiegazione del seguente problema di geometria con due o più incognite

  • Il perimetro di un trapezio isoscele è cm 92; il lato obliquo è il doppio della base minore e la differenza fra i 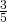\frac 3 5 del lato obliquo e la sesta parte della base maggiore è la metà della base minore. Calcolare l’area del trapezio.

Chiamiamo con x la base maggiore, con y la base minore e con z il lato obliquo:

\Bigg\{ \begin{array}{l} x+y+2z=92 \\ z=2y \\ \frac 35z - \frac 16x = \frac 1 2 y \end{array}

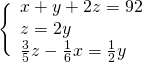
Sostituiamo subito il valore della z nelle altre due.

\Bigg\{ \begin{array}{l} x+y+2(2y)=92 \\ z=2y \\ \frac 35 (2y) - \frac 16x = \frac 1 2 y \end{array}

\Bigg\{ \begin{array}{l} x+5y=92 \\ z=2y \\ \frac {36y-5x}{30} = \frac {15}{30} y \end{array}

\Bigg\{ \begin{array}{l} x+5y=92 \\ z=2y \\ 36y-5x = 15 y \end{array}

\Bigg\{ \begin{array}{l} x=92-5y \\ z=2y \\ 36y-5(92-5y) -15y=0 \end{array}

\Bigg\{ \begin{array}{l} x=92-5y \\ z=2y \\ 36y+25y -15y-460=0 \end{array}

\Bigg\{ \begin{array}{l} x=92-5y \\ z=2y \\ 46y =460 \end{array}

\Bigg\{ \begin{array}{l} x=92-5\cdot 10 \\ z=2\cdot 10 \\ y =10 \end{array}

\Bigg\{ \begin{array}{l} x=42 \\ z=20 \\ y =10 \end{array}

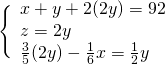
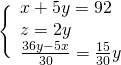
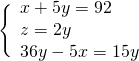
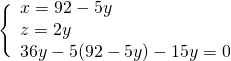
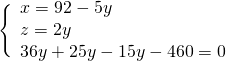
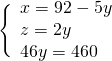
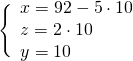
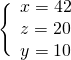
Per trovare l’altezza dovremo sfruttare il triangolo rettangolo che si viene a formare tracciando l’altezza sulla base maggiore, ove si forma un segmento che risulta essere la semidifferenza tra le due basi:

h=\sqrt {(20^2-(\frac {42-10}{2})^2}=\sqrt {400-256}=\sqrt {144}=12 \mbox { cm}

Quindi per calcolare l’area basterà applicare la formula con i valori appena trovati:

 

A=\frac {(42+10)\cdot 12}{2}=312 \mbox { cm}^2

 

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 445 persone)

Lascia un commento