Un equazione algebrica di 2° grado si presenta nella forma: ![]() .
.
» Se ![]() l’equazione si dice in forma completa e si risolve utilizzando la formula risolutiva:
l’equazione si dice in forma completa e si risolve utilizzando la formula risolutiva:
![]()
si dice discriminante;
- se
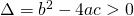 esistono due soluzioni reali e distinteche si ottengono applicando la formula risolutiva
esistono due soluzioni reali e distinteche si ottengono applicando la formula risolutiva - se
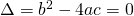 esistono due soluzioni reali e coincidenti
esistono due soluzioni reali e coincidenti 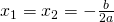
- se
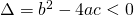 esistono due soluzioni complesse e coniugate.
esistono due soluzioni complesse e coniugate.
» Se ![]() l’equazione si dice pura e diventa
l’equazione si dice pura e diventa ![]() .
.
Le due soluzioni sono ![]()
» Se ![]() l’ equazione si dice spuria e si risolve raccogliendo
l’ equazione si dice spuria e si risolve raccogliendo ![]() per cui le soluzioni sono
per cui le soluzioni sono ![]()
» Formula ridotta
Se b è pari, può essere più comodo applicare la formula risolutiva ridotta:
![]()
» Relazione tra le soluzioni e i coefficienti a, b, c dell’equazione:
![]() ,
, ![]()
![]()
» Scomposizione del trinomio di 2° grado:
![]()
Altri hanno visualizzato anche:
- Proprietà delle operazioni
- Proprietà delle potenze
- Prodotti notevoli
- Fattorizzazione
- Equazioni di primo grado
- Radicali
- Equazioni di secondo grado
- Disequazioni irrazionali
- Logaritmi
(Questa pagina è stata visualizzata da 229 persone)