Salve, avrei un problema quando risolto il sistema mi trovo davanti questo :
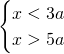
come si procede?
grazie
SOLUZIONE
Bisognerà distinguere casi differenti, in base al segno di ![]() .
.
Se ![]() , immaginatelo come un numero, che so,
, immaginatelo come un numero, che so, ![]() …. il sistema sarebbe questo:
…. il sistema sarebbe questo:
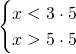
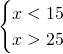
Si vede chiaramente che questo sistema è impossibile, senza bisogno di fare il grafico…
Stesso discorso dicasi per ![]() , difatti avremmo:
, difatti avremmo:
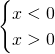 ,
,
anche questo impossibile…
Se invece fosse ![]() , immaginate sia uguale a
, immaginate sia uguale a ![]() , otterremmo:
, otterremmo:
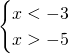
che implica che la soluzione sia :
![]() ;
;
generalizzando alla soluzione letterale, otteniamo la soluzione del sistema:
![]() .
.
(Questa pagina è stata visualizzata da 238 persone)