Esercizio 3 Sistemi in cui compaiono disequazioni frazionarie o di grado superiore al primo

0

Traccia

\begin{cases} \frac {x+7}{x-2}<\frac 12 \\ \frac {x-5}{5} \geq \frac {x+7}{7} \end{cases}

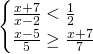
Svolgimento

\begin{cases} \frac {x+7}{x-2}-\frac 12<0 \\ 7(x-5) \geq 5(x+7) \end{cases}

\begin{cases} \frac {2x+14-x+2}{2(x-2)}<0 \\ 7x-35 \geq 5x+35 \end{cases}

\begin{cases} \frac {x+16}{2(x-2)}<0 \\ 2x \geq 70 \end{cases}

\begin{cases} \frac {x+16}{2(x-2)}<0 \\ x \geq 35 \end{cases}

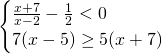
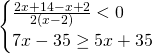
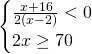
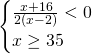
Per la prima disequazione dobbiamo innanzitutto considerare il risultato nel complesso, quindi:

  • N > 0 \Rightarrow x > -16
  • D>0 \Rightarrow x>2
(-\infty;-16) (-16;2) (2;+\infty)
N > 0 —- +++ +++
D>0 —- —- +++
Ris +++ —- +++

Inserendo il risultato nel sistema otteniamo:

 

\begin{cases} -16<x<2 \\ x\geq 35 \end{cases}

 

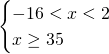
Facendo il grafico dell’intero sistema otteniamo:

(-\infty;-16) (-16;2) (2;35] [35;+\infty)
I +++
II  +++
Ris

 

da cui si evince che non esisterà soluzione, ovvero il sistema è impossibile.

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 97 persone)

Lascia un commento