Corpo del messaggio:
mi servirebbe la risoluzione a queta equazione con il metodo che preferite (basta che ne sono 2) grazie mille anticipatamente

 

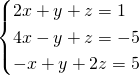
Soluzione

Per semplificare le operazioni usiamo il metodo di riduzione, addizionando la prima alla seconda equazione, la seconda alla terza e lasciando la terza inalterata:

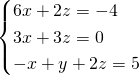
Riscriviamo le prime due semplificandole:

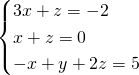
Dalla seconda troviamo la , e sostituiamo nella prima:

 

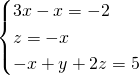
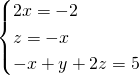
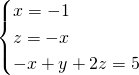
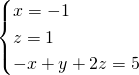
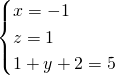
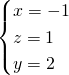
Se ti servono altri metodi, dimmi quali hai usato, ad esempio quello del determinante delle matrici, che te lo sviluppiamo subito

(Questa pagina è stata visualizzata da 625 persone)