Traccia

Svolgimento

Dovendo analizzare la positività del valore assoluto, andremo a discutere due sistemi in maniera parallela e, infine, uniremo le eventuali soluzioni accettabili.

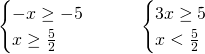
Da qui avremo le soluzioni dei due sistemi di cui:

1. 
2. 

Unendo ambedue le soluzioni otteniamo la soluzione della disequazione iniziale:

 

 

Altri esercizi simili:

• Esercizio 1 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 2 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 3 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 4 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 5 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 6 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 7 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 8 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 9 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita
• Esercizio 10 Disequazioni in cui figurano valori assoluti di espressioni contenenti l’incognita

(Questa pagina è stata visualizzata da 97 persone)