Esercizio 1 Sistemi simmetrici di grado superiore al secondo

Traccia

$\begin{cases} x^2+y^2=29 \\ xy=-10 \end{cases}$

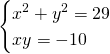
Svolgimento

Per risolvere questo sistema bisogna prima di tutto ricondurlo in una forma particolare ricordando che:

$x^2+y^2=(x+y)^2-2xy$ ,

da cui avremo:

$\begin{cases} (x+y)^2-2xy=29 \\ xy=-10 \end{cases}$

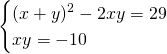
Sostituendo ora il valore di $xy$ otteniamo:

$\begin{cases} (x+y)^2+20=29 \\ xy=-10 \end{cases}$

$\begin{cases} (x+y)^2=9 \\ xy=-10 \end{cases}$

$\begin{cases} x+y=\pm3 \\ xy=-10 \end{cases}$

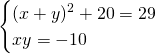
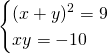
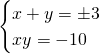
Quindi avremo:

$\begin{cases} x+y=-3 \\ xy=-10 \end{cases} \qquad \lor \qquad \begin{cases} x+y=3 \\ xy=-10 \end{cases}$

che ammetteranno le due equazioni:

$z^2+3z-10=0 \qquad \lor \qquad z^2-3z-10=0$

che daranno come soluzioni:

$z_1= -5 \quad \lor \quad z_2=2 \quad$ la prima equazione e

$z_3= 5 \quad \lor \quad z_4=-2 \quad$ la seconda equazione.

Le 4 coppie di soluzioni saranno:

$(-5,2); (2,-5);(5,-2);(-2,5).$

Altri esercizi simili:

(Questa pagina è stata visualizzata da 349 persone)

Matebook