Christian: Risoluzione Sistemi A 3 incognite a 3 equazioni 1

Pubblicato il da EdoLascia un commento
0

Corpo del messaggio:
Salve mi servirebbe la risoluzione a questi 2  sistemi con tre incognite e tre equazioni con i 3 metodi ( se e possibile 🙂 ) ( Cramer,Pivot,Sostituzione ) anche  un solo metodo e benvoluto

Confido in voi grazie mille

Di seguito i sistemi

\begin{cases} x+\frac 12y +\frac 13z=4 \\ x+y+z=6 \\ \frac 13 x+\frac 12y+z=4 \end {cases}

 

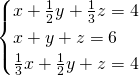
Soluzione:

Innanzitutto, calcolando i minimi comuni multipli sulla prima e la terza equazione rendiamo tutti i coefficienti interi, in modo da semplificare i calcoli, e dopo svolgeremo i sistemi con i metodi di sostituzione e di Cramer.

\begin{cases} \frac {6x+3y+2z}{6}=\frac {24}{6} \\ x+y+z=6 \\ \frac {2x+3y+6z}{6}=\frac {24}{6} \end {cases}

 

\begin{cases} 6x+3y+2z=24 \\ x+y+z=6 \\ 2x+3y+6z=24 \end {cases}

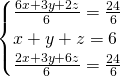
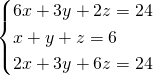
  • Metodo di sostituzione

Troviamo la x nella seconda equazione e sostituiamola nelle altre 2 equazioni:

\begin{cases} 6(6-y-z)+3y+2z=24 \\ x=6-y-z \\ 2(6-y-z)+3y+6z=24 \end {cases}

\begin{cases} 36-6y-6z+3y+2z=24 \\ x=6-y-z \\ 12-2y-2z+3y+6z=24 \end {cases}

\begin{cases} -3y-4z=-12 \\ x=6-y-z \\ y+4z=12 \end {cases}

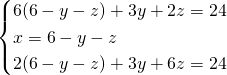
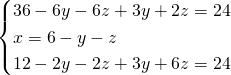
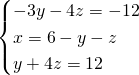
Dall’ultima ricaviamo la y :

\begin{cases} -3(12-4z)-4z=-12 \\ x=6-(12-4z)-z \\ y=12-4z \end {cases}

\begin{cases} -36+12z-4z=-12 \\ x=6-12+4z-z \\ y=12-4z \end {cases}

\begin{cases} 8z=24 \\ x=3z-6 \\ y=12-4z \end {cases}

\begin{cases} z=3 \\ x=9-6=3 \\ y=0 \end {cases}

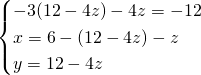
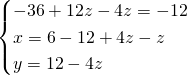
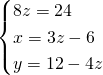
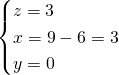
  • Metodo di Cramer

Utilizziamo il sistema iniziale:

\Delta =\begin{vmatrix} 1 & \frac 12 & \frac13 \\ 1 & 1 & 1 \\ \frac 13 & \frac 12 & 1 \end{vmatrix}=(1+\frac16 +\frac 16)-(\frac 19+\frac 12+\frac 12)=1+\frac13-\frac 19-1=\frac {3-1}{9}=\frac 29

\Delta_x =\begin{vmatrix} 4 & \frac 12 & \frac13 \\ 6 & 1 & 1 \\ 4 & \frac 12 & 1 \end{vmatrix}=(4+2+1)-(\frac 43+2+3)=7-\frac {19}{3}=\frac {21-19}{3}=\frac 23

\Delta_y =\begin{vmatrix} 1 & 4 & \frac13 \\ 1 & 6 & 1 \\ \frac 13 & 4 & 1 \end{vmatrix}=(6+\frac43 +\frac 43)-(\frac 69+4+4)=6+\frac83-\frac 23-8=2-2=0

\Delta_z =\begin{vmatrix} 1 & \frac 12 & 4 \\ 1 & 1 & 6 \\ \frac 13 & \frac 12 & 4 \end{vmatrix}=(4+1+2)-(\frac 43+3+2)=7-\frac {19}{3}=\frac {21-19}{3}=\frac 23

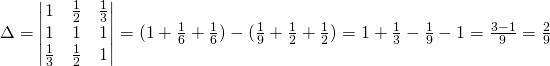
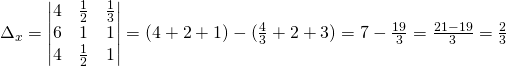
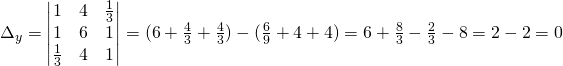
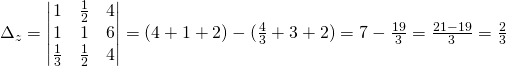
Da cui avremo le 3 soluzioni:

  • x=\frac {\Delta_x}{\Delta}=\frac {\frac 23}{\frac 29}=\frac 23 \cdot \frac 92=3
  • y=\frac {\Delta_y}{\Delta}=\frac {0}{\frac 29}=0
  • z=\frac {\Delta_z}{\Delta}=\frac {\frac 23}{\frac 29}=\frac 23 \cdot \frac 92=3

Se fosse necessario anche il metodo Pivot, basta chiedere… 🙂

(Questa pagina è stata visualizzata da 539 persone)

Lascia un commento