Soluzione e svolgimento dei seguenti sistemi di disequazioni
Traccia
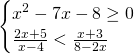
Svolgimento
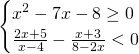
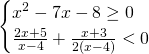
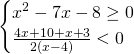
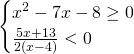
Analizziamo singolarmente le due disequazioni:
Bisogna prima di tutto calcolare il ![]() :
:
![]() .
.
Andando a vedere la tabella in
vedremo che questa disequazione, andando a trovare la soluzione dell’equazione associata, sarà verificata:
![]()
Andiamo ad analizzare numeratore e denominatore singolarmente:
| I | —- | +++ | +++ |
| II | —- | —- | +++ |
| Risultato | +++ | —- | +++ |
![]()
Inserendo tutto nel grafico avremo:
| I | +++ | +++ | +++ | ||
| II | +++ | +++ | |||
| Risultato | +++ |
Essendo un sistema, bisognerà prendere in considerazione solo i risultati in comune ad ambedue le disequazioni, quindi il risultato sarà:
![]()
Altri esercizi simili:
- Esercizio 1 Sistemi di disequazioni di grado superiore al primo
- Esercizio 2 Sistemi di disequazioni di grado superiore al primo
- Esercizio 3 Sistemi di disequazioni di grado superiore al primo
- Esercizio 4 Sistemi di disequazioni di grado superiore al primo
- Esercizio 5 Sistemi di disequazioni di grado superiore al primo
- Esercizio 6 Sistemi di disequazioni di grado superiore al primo
- Esercizio 7 Sistemi di disequazioni di grado superiore al primo
- Esercizio 8 Sistemi di disequazioni di grado superiore al primo
- Esercizio 9 Sistemi di disequazioni di grado superiore al primo
(Questa pagina è stata visualizzata da 300 persone)