Esercizio 1 Valori assoluti: disequazioni in cui compaiono valori assoluti

-3

Soluzione e svolgimento della seguente disequazione con valore assoluto

Traccia

3 < \left | x^2-1 \right |

Svolgimento

Per svolgere queste disequazioni basterà studiare due sistemi separati e poi unire le soluzioni. Innanzitutto studiamo la positività del modulo, dove per comodità, trascriviamo solo il risultato:

  • x^2-1 \geq 0 \Rightarrow x \leq -1 \quad \lor \quad x \geq 1

 

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ 3<x^2-1 \end{cases} \qquad \begin{cases} -1<x<1 \\ 3<1-x^2 \end{cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x^2-4>0 \end{cases} \qquad \begin{cases} -1<x<1 \\ x^2+2<0 \end{cases}

\begin{cases} x \leq -1 \quad \lor \quad x \geq 1 \\ x<-2 \quad \lor \quad x>2 \end{cases} \qquad \begin{cases} -1<x<1 \\ \mbox { impossibile } \end{cases}

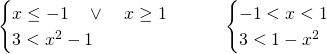
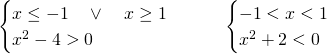
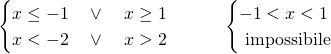
Quindi, nel primo sistema la soluzione è accettabile perchè rispetta le condizioni, mentre invece il secondo sistema è impossibile.

La soluzione dell’esercizio iniziale è quindi:

x<-2 \quad \lor \quad x>2.

 

 

Altri esercizi simili:

(Questa pagina è stata visualizzata da 334 persone)

Lascia un commento