Esercizi disequazioni di grado superiore al secondo 5

$x^4-5x^2+4<0$

Analizziamo l’equazione associata:

$x^4-5x^2+4=0$

Essendo una biquadratica possiamo riportarla come prodotto di due fattori di secondo grado, notando che è un trinomio particolare dove le due radici devono dare come somma $-5$ e come prodotto $4$ , quindi:

$x^4-5x^2+4=(x^2-4)(x^2-1)$ ;

ma anche questi sono scomponibili in fattori di primo grado, quindi:

$x^4-5x^2+4=(x-2)(x+2)(x-1)(x+1)$

La disequazione diventerà:

$(x-2)(x+2)(x-1)(x+1)<0$

Analizzando pezzo per pezzo otteniamo:

$x-2>0 \, \, \Rightarrow \, \, x>2$
$x+2>0 \, \, \Rightarrow \, \, x>-2$
$x-1>0 \, \, \Rightarrow \, \, x>1$
$x+1>0 \, \, \Rightarrow \, \, x>-1$ .

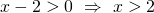
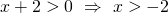
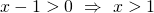
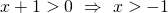Unendo tutti i risultati avremo:

	$(-\infty;-2)$	$(-2;-1)$	$(-1;1)$	$(1;2)$	$(2;+\infty)$
$x-2>0$	—-	—-	—-	—-	+++
$x+2>0$	—-	+++	+++	+++	+++
$x-1>0$	—-	—-	—-	+++	+++
$x+1>0$	—-	—-	+++	+++	+++
	+++	—-	+++	—-	+++