Esercizio 21 Disequazioni irrazionali relazionate da polinomio

0

Traccia

x\geq \sqrt{x^2-4}-4

\sqrt{x^2-4} \leq x+4

Svolgimento

Avendo una radice quadrata minore di un polinomio avremo necessità di lavorare solo su un sistema, imponendo determinate condizioni:

\begin{cases} x^2-4 \geq 0 \\ x+4 \geq 0 \\ x^2-4 \leq x^2+8x+16 \end{cases}

\begin{cases} x^2-4 \geq 0 \\ x \geq -4 \\ 8x+20 \geq 0 \end{cases}

\begin{cases} x^2-4 \geq 0 \\ x \geq -4 \\ x \geq -\frac 52 \end{cases}

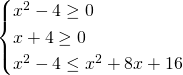
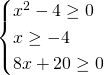
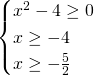
Senza bisogno di fare grossi calcoli possiamo direttamente dire che la terza disequazione è verificata per

    \[x \leq -2 \quad \lor \quad x \geq 2\]

Unendo

\begin{cases} x \leq -2 \quad \lor \quad x \geq 2 \\ x \geq -4 \\ x \geq -\frac 52 \end{cases}

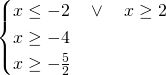
Mettendo a sistema le soluzioni, otterremo subito che la soluzione sarà:

    \[ -\frac 52 \leq x \leq -2 \quad \lor \quad x \geq 2\]

.

 

 

Altri esercizi simili

 

(Questa pagina è stata visualizzata da 108 persone)

Lascia un commento